●Subroutine: DECOMPVT●
![]() を[L][D][L]Tに分解します。計算が終了
すると、GSMTX(I,1)に[D]、それ以外は[L]Tになっています。生成されている
を[L][D][L]Tに分解します。計算が終了
すると、GSMTX(I,1)に[D]、それ以外は[L]Tになっています。生成されている
![]() は
対称Multi-Diagonal Matrixになって
いるため、[L][D][L]T分解の計算は少々複雑です。
詳細についてはLU Decompositionのプログラミングの対称バンドマトリクスの場合を参考にして下さい。
は
対称Multi-Diagonal Matrixになって
いるため、[L][D][L]T分解の計算は少々複雑です。
詳細についてはLU Decompositionのプログラミングの対称バンドマトリクスの場合を参考にして下さい。
引数のNNODE,NBWDTHMXW,MXNについては既に上で説明しましたので省きます。
| 変数名 | タイプ | 配列 | 意味/目的 |
|---|---|---|---|
| GSMTX | 実数 | 2次元 | 計算前は |
●Subroutine: LANCSEQU●
Subroutine: ATIMESU1とSubroutine: LANCZOSをコントロールします。変数名の働きについては、
ATIMESU1とLANCZOSを見て下さい。
●Subroutine: ATIMESU1●
このサブプログラムはLanczos法の[A]{U1}を計算します。
詳細については、●(2) [A]{U1}の計算を見て下さい。
引数のMXENGN,MXN,MXW,NNODE,NBWDTH,GEOM,VEC,GSMTXについては既に上で説明しましたので省きます。
| 変数名 | タイプ | 配列 | 意味/目的 |
|---|---|---|---|
| IEIGN | 整数 | なし | モードを意味します。1からNEIGEN変化します |
| U1 | 実数 | 1次元 | [A]{y} |
●Subroutine: LANCZOS●
Subroutine: ATIMESU1からU1を受け取り、残りのLanczos手順(3)から(6)
と残りのLanczos手順(7)から(12)を計算します。
全てのモードにつて計算が終了すると、全ての正規直交ベクトルの集合体マトリクス[V]と[T]マトリクスが出来上がります。
引数のMXN,MXENGN,NNODE,IEIGN,U1,NEIGEN,VECについては既に上で説明しましたので省きます。
| 変数名 | タイプ | 配列 | 意味/目的 |
|---|---|---|---|
| SUBSMTX | 実数 | 2次元 | [T]マトリクスのこと |
●Subroutine: EIGENVEC●
Jacob法で[T]から部分空間の固有値λkと部分空間の固有ベクトル{ξk}を計算します。
部分空間の固有値は、実空間の固有値と同じですが、シフトパラメーター分ずれて
います。部分空間の固有ベクトル{ξk}を実空間の[A]{y}=λ{y}に戻すには、
{yk}=[U]{ξk}を計算しなければなりません。更に、
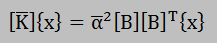 の問題に戻すには、
[B]T{xk}={yk}から{xk}を計算しなければなりません。
の問題に戻すには、
[B]T{xk}={yk}から{xk}を計算しなければなりません。
引数のMXN,MXENGN,DELTA,NNODE,GEOM,SUBSMTX,VEC,NEIGENについては既に上で説明しましたので省きます。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |