この方法は、六面体1 次要素で離散化していることを前提としています。つまり、上の平方 根が実数計算出来なければなりません。高次の要素になると[M]が正定値でなくなる場合 があります。その場合は、[M]を複素数で表します。この問題が発生するのを避けるために、 [M]をランピングするという方法があります。私のプログラムでは、このランピングを 採用しています。
三角行列に分解した[M]を、シフトパラメーターを導入した定義式に代入します。すると、以 下が得られます。
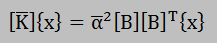
次に、上式の両辺に左から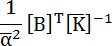 を掛けます。すると、以下が得られます。
を掛けます。すると、以下が得られます。
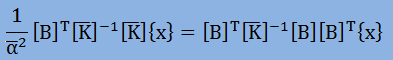
そして、以下の定義を導入します。
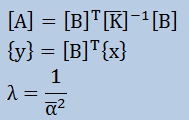
すると、以下の固有値問題の一般形の式が得られます。
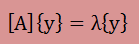
ここまで到達できれば後は上式を部分空間に射影し、Lanczos 法で固有値を計算するのみです。
また、[A]には![]() -1が含まれていますが、
以前に紹介したインバースを計算しない方法で計算をすすめます。そのためには、
-1が含まれていますが、
以前に紹介したインバースを計算しない方法で計算をすすめます。そのためには、
![]() を下に示す三角行列分解をする必要があります。
を下に示す三角行列分解をする必要があります。
■Lanczos法■
前にも説明しましたが、Lanczos 法は、上で説明した正規直交マトリクス[U]と部分空間に射影された
三角対角行列[T]を合理的に生成する1つの方法です。計算手順は、以下のようになります。
●(1) 初期正規直交ベクトル{U1} の生成
求めたい固有値の数(m)とシフトパラメーター(δ)を決めます。そして、初期正規直交ベクト
ル{U1}を作ります
(Eigen&Lanczosの{u1}と同じです)。
ベクトルの長さは、1でなくてはなりません。つまり、√({U1}T{U1})=1。
{U1}の作り方ですが、乱数表等を用いて{U1}を生成することが可能です。実際、πを必要桁まで計算し、
数桁づつを乱数として、{U1}を計算しても固有値を問題なく得ることができます。しかし、最も手軽な
方法として、剛性マトリクスの対角要素が使われています。ここでも対角要素を使いました。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |