■対称円筒座標の線形弾性解析■
有限要素法が出始めたころは、計算機のメモリーが少なかったために何とか無理やり計算領域を軸対称にして解析を実施していました。例えば、領域が中心面を境に対称だったとすると、計算対象領域は半分になります。それが筒や円柱の場合、軸対称として取り扱えるようになり、計算領域はカット面の半分の二次元ですむことになります。今や計算能力は格段に上がり詳細な解析が可能になりました。
しかし、大がかりな計算を行う前に、計算結果の予測をしておくことは必要です。そうでないと、せっかく計算が終了しても、解が正しいのかどうかが解りません。こんな時に役立つのが計算領域を簡略化し予測用の計算を事前にしておくことです。できれば手計算でね。
ここでは、線形弾性解析が円筒座標系でどのように書き表されているか、そして有限要素法はどのように出来ているのかを勉強してみます。そして、2つの計算例を紹介します。
■理論的背景■
これまでは、全ての技術問題をxyz座標系で話をしてきました。ここでは、円筒座標つまりrθzが座標軸になります。円筒座標系の発散の定理や支配方程式になれてもらうために、解析学と材料力学から話をすすめたいと思います。まず、円筒座標系ですが、下図をみて下さい。
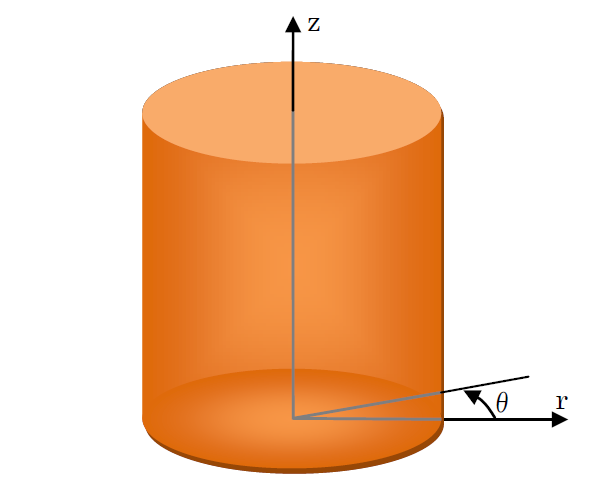
ここでは最終的にθ方向の応力の変化の無いz軸対称の状況を考慮し式の展開を行いますが、支配方程式、応力の式、ひずみの式の何の項が消えたのかを確認するために、円筒座標系のフルの数式の展開を行います。 弾性解析の支配方程式を導くためには、変位(displacements)、ひずみ(strains)、応力(stresses)を定義しなければなりません。以下は、円筒座標系での微小変形をベースにした変位、ひずみ、応力です。
まず変位は以下のように定義しておきます。書物等によると別の記述が使われていますので、注意して下さい。
半径(r)方向の変位 :u
円筒(θ)方向の変位:v
長手(z)方向の変位 :w
ひずみには法線方向と接線方向が有ります。半径、円筒、長手方向の法線ひずみは次のようになります。詳細についてはPage668, Introduction to the Mechanics of a Continuous Medium, Prentice Hall, 1969参考にして下さい。
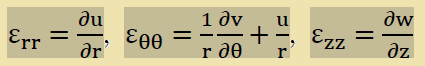
| Solid Eigen | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |