そして接線方向のせん断ひずみ角度は以下になります。導出方法については力学の本を参考にして下さい。
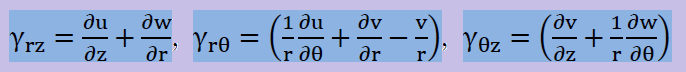
法線方向の応力はGeneralized Hooke's Lawによって決定されています。次のように書けます。
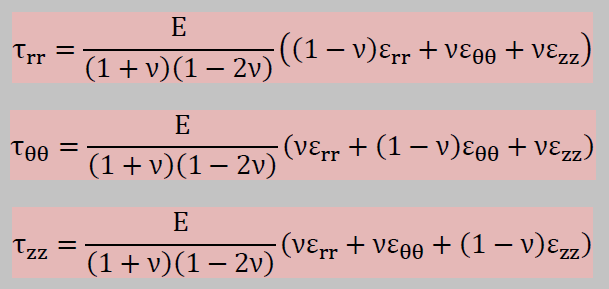
ひずみ角度によるせん断応力は定義により次のように書けます。
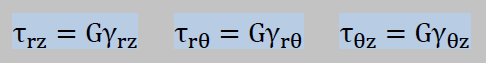
これで式を導く全ての材料が揃いました。次にやることはNewtonの第2法則を領域型で書き表したNavierの方程式を円筒座標系で表すことです。円筒座標系の微小体積に作用する応力のバランスを軸毎に取ると以下のようになります。導出については文献 Introduction to the Mechanics of a Continuous Medium, Prentice Hall, 1969, Page 668 をチェックしてみて下さい。
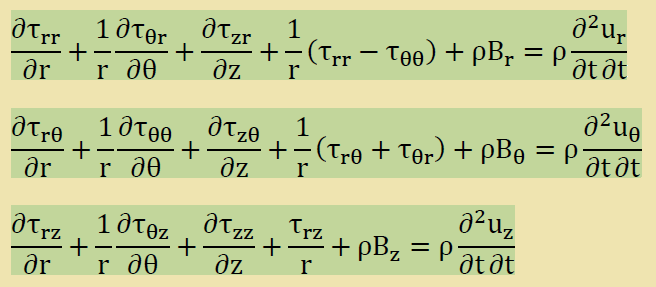
ここまでは、3次元の弾性体の運動方程式を円筒座標系で書いたにすぎません。これから先は上の式を軸対称の静的弾性解析用の方程式にしなければなりません。 仮定としてまず、ここでは自重を無視し平衡状態の弾性体について勉強するので、上式にあるBiと右辺はゼロとします。そして、z軸中心の軸対称が今回の目的ですので、∂τθθ/∂θ=0, τrθ=0, τθz=0, ∂v/∂θ=0が成り立ちます。しかし、τθθは存在するのでオミットできません。 結果的にひずみは以下のように簡略化されます。
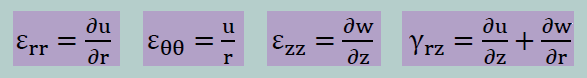
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |