すると上のひずみをGeneralized Hooke’s Lawに代入すると、応力は以下のように書けます。

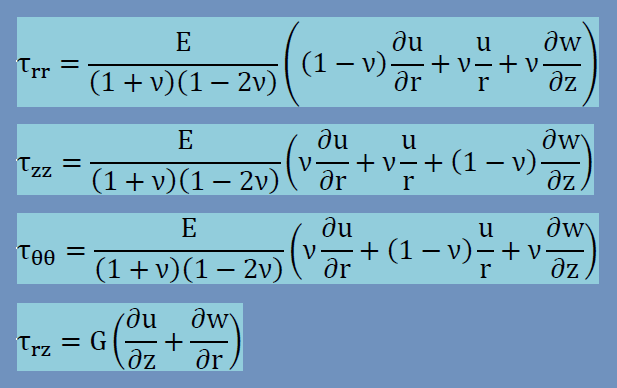
Navierの方程式も以下のようにシンプルに成ってきます。

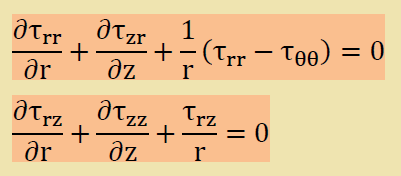
次にやらなければならない事は、上の2つ式を有限要素法で離散化しグローバル剛性マトリクス[K]をアッセンブルすることです。そして、境界条件を与え変位(u,w)を計算しなければなりません。変位が得られればひずみと応力はこれまでに説明してきた式で簡単に計算できます。

■円筒座標系における発散の定理■
支配方程式(ここでは上のNavierの式)を重み付け残差法等で有限要素式に変換するには、発散の定理が必要になります。円筒座標系の発散の定理は下に示すようにちょっと変わった格好をしています。特に右辺のｒでの微分項に注意して下さい。

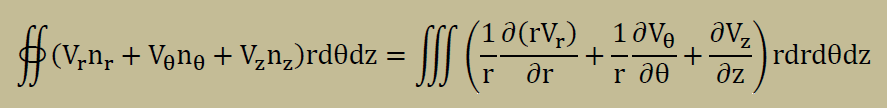
■重み付け残差法■
これで有限要素法の数式展開を行うための全ての材料がそろいました。ということで、Navierの式の式を重み付け残差法のルールに従って積分式Iを書くと以下になります。ここまでは、これまでの重み付け残差法と同じです。

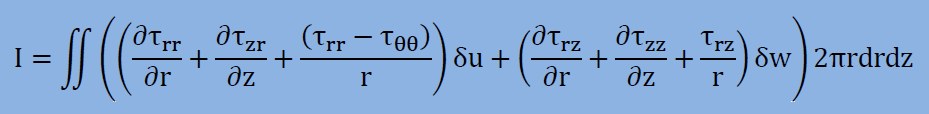
上に示した発散の定理を積分式Iのδuがらみの半径方向(r)の微分に適用すると、以下のことが言えます。ただし、τ_θθの項は発散の定理から導き出されていないので、そのまま積分式Iに残留します。この項(-τ_θθ/r)は、力のバランスより得られた項ですので注意して下さい。