弾性解析のFEMプログラミングで一番やっかいなのが要素剛性マトリクスの生成とグローバル剛性マトリクスへのAssemblyです。2次元でも大変でした。3次元はもっと大変になります。 この剛性マトリクスですが、プログラムに書き下ろすとかなり複雑になります。しかし、手順を踏まえれば問題なくプログラミングできますので安心して下さい。ここでは、その計算手順とグローバル剛性マトリクス[K]に足しこむ操作(assembly)を紹介します。 そこら辺を念頭において学習をしてみて下さい。
■要素剛性マトリクスのプログラミング■
まず、行わなければならないのが[B]T[D][B]の展開です。ここでは、要素単位の剛性マトリクスを[k]= [B]T[D][B]で表すことにします。すると[k]は、3次元8節点要素を用いた場合、24×24のサイズになります。展開の前に、準備しておかなければならないのが、以下の形状関数の微分です。
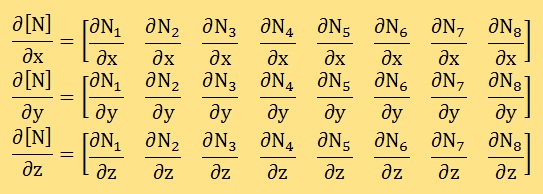
Iso-Parametric要素のところでも説明しましたが、形状関数[N]は無次元座標の独立変数(ξ,η,ζ)での微分は簡単にできますが、x, y, zでの微分には、Jacobianマトリクスを準備しておく必要があります。つまり、[N]のx, y, zでの微分を得るには、以下の式を解く必要があります。以下の式は、無次元座標値が与えられればいつでも計算できます。
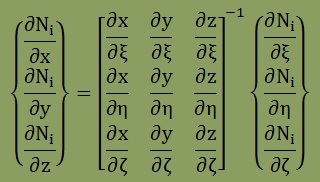
形状関数の微分の計算方法が分かったところで、[k]= [B]T[D][B]の展開を行ってみましょう。以下は、[D]に等方性材料が考慮してあります。
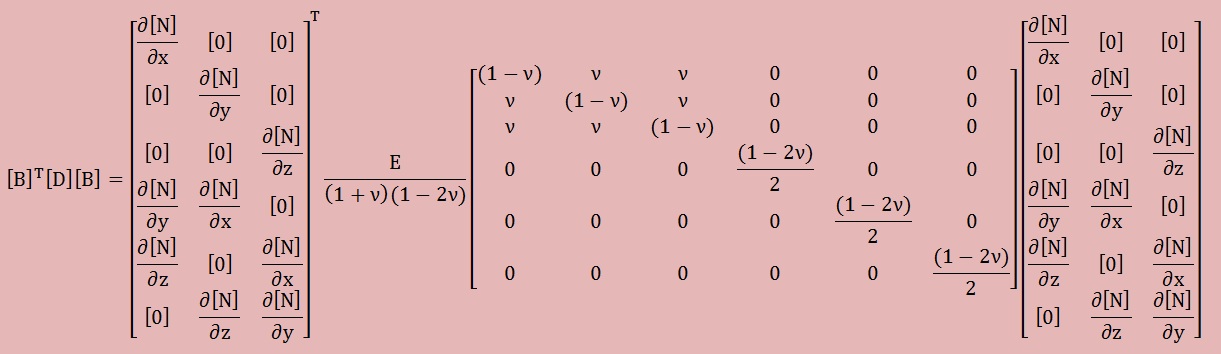
| LU Decompo | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |