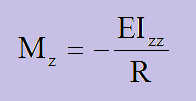
ここに、E=ヤング係数[Pa=N/m²]、I_zz=曲げられる方向の断面2次モーメント[m⁴]です。 そしてビーム変位(y)が盛り上がり円弧を解にもつ微分方程式は、以下で書けます。この場合、2階微分は負になっていることに注意して下さい。

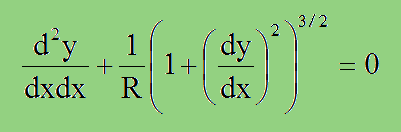
また、ビーム変位(単位[m])の勾配(dy/dx)の二乗が小さいと仮定できれば、ビーム変形と半径がRとで以下の関係があります。

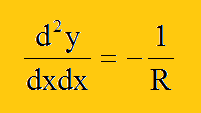
ここら辺の式の展開については、1次元のHelmholtz Equationも参考にして下さい。 注意：下図に示すように、ビームが下方向に垂れる場合(通常の梁が重力による変形)の円の方程式とモーメントの関係式ですが、上で説明した関係は使えません。

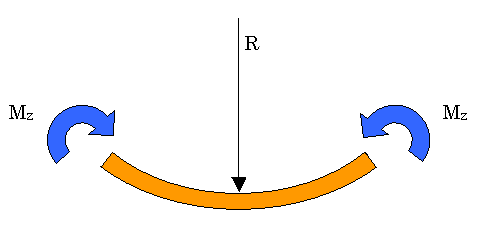
円の方程式とモーメントの関係式は、以下になります。符号に注意して下さい。

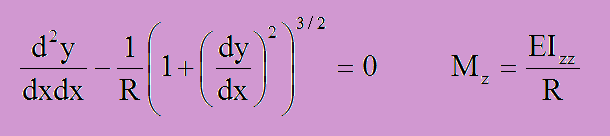
上の式で値が正または負になりうる項は、d²y/dxdxとM_zのみです。R, (dy/dx)², E, I_zzは、負になりえません。ですから、ビームの変形状況(上開き、下開き)によって式中の符号を変える必要があります。しかし、上の2つの式を合体させるとビームの変形状況(上開き、下開き)に関係なく以下の式が得られます。