よって、運動方程式は以下の左になり、また以下の右のようにも書けます。

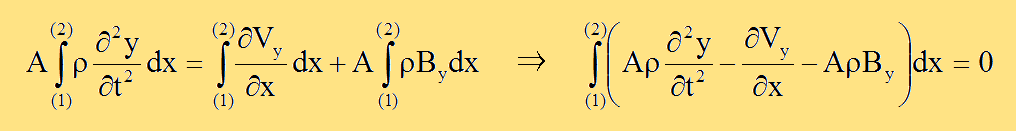
領域の任意性を考慮すると、以下に示す力収支方程式になります。任意性とは、(1)から(2)までの距離が変化しても上の式は成り立つと いうことです。

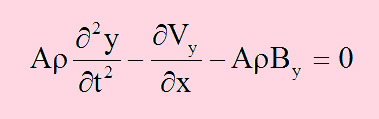
次元を1次に落としたことにより、ビームにはせん断力(V_y)以外に曲げモーメント(M_z)という量が使われています。この曲げモーメント(M_z)は、せん断しようとしている力(V_y)を積分することにより得ることができます。つまり、以下の関係が成立します。

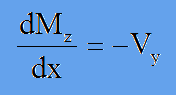
そして、上式の両辺を再度微分すると、d2Mz/dx2=-dVy/dxになります。よって、運動方程式は、以下のようにも書けます。

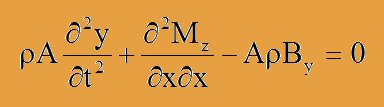
前に進む前に梁の変位とモーメントの関係を確認しておきます。下図に示すように、梁の両端に曲げモーメント(M_z)が作用していると、ビームは半径Rの円弧を描きます。

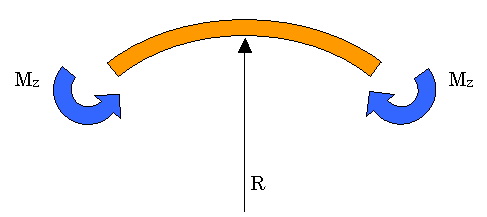
このことは、ビーム断面に働くモーメントと外力によるモーメントの釣り合いをとると、モーメントの関係式は以下になります。ここでは、ビームが盛り上がる方向に変形すると仮定しています。