上図を参考にしながら、上式の積分式を長さdxの1次元ビームに置き換えると以下のようになります。上下方向(y)の変位を座標軸と同じyで表すことにします。
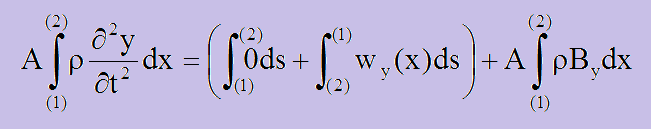
変位yに使うシンボルですが、一般にはy軸方向の変位にvを用いますが、これだとせん断力を表すシンボルと同じになってしまいます。また、縦方向ということで、wが使えますが、これも荷重w(x)と混同してしまいます。結果、yを使うことにしました。
下図を見て下さい。ビームの下面((1)→(2))には荷重がないため境界積分をしても結果はゼロです。しかし、上面((1)←(2))には荷重がるため積分に結果が残ります。
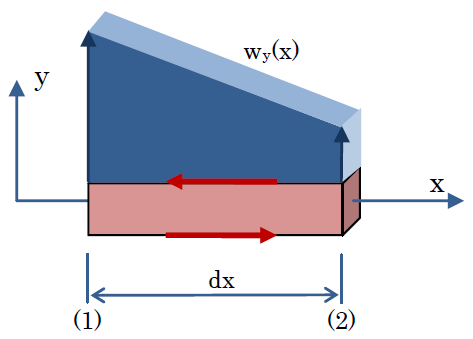
ところで、上式の右辺の第1項は、もともと境界積分ですので、積分子はdsで表しています。これを領域積分風に書けば以下になります。1次元の話になると、境界積分と領域積分の違いが無くなります。貴方は、各積分の元は何であったかを注意して式の展開を見て下さい。
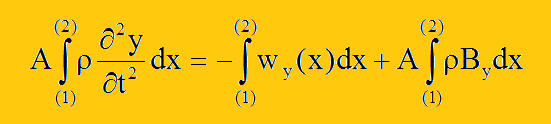
荷重wy(x)を積分した量は、せん断力の増減に現れてきます。つまり、せん断力の定義を用いると、上式を以下のように書き換えることもできます。
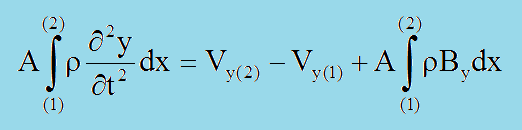
ビームの場合、境界は両端のみに存在します。したがって、ビームの途中に作用している外力(wy(x)[N/m])は、式の導出上、領域内で作用している力になってしまいます。そして、せん断力Vyと外力wyとでは、上の2つの式から以下の関係があることが分かります。
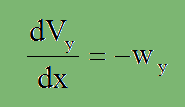
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |