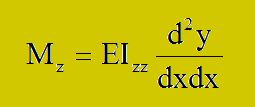
そして、上式を微分方程式に代入すると、以下が導き出されます。
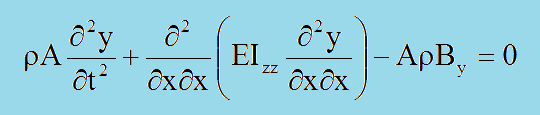
ここで、外力のAρByをゼロと置き、ビームの変位y(x,t)の厳密解を解いてみましょう。
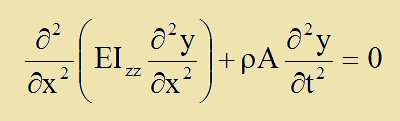
微分方程式の解き方で変数分離(separation of variables)と言う方法があります。ここでも使ってみましょう。変位y(x,t)をy(x,t)=Y(x)T(t)で変数分離してみます。Y(x)はxのみの関数で、T(t)はtのみの関数です。上式のyにY(x)T(t)を代入しちょっと変形すると以下のように書けます。
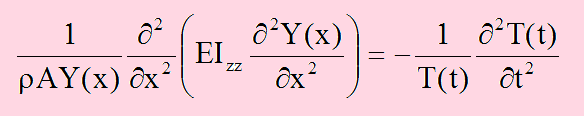
左辺が空間の(x)のみを引数とする式で右辺が時間の(t)だけの式になっています。それらが=で結ばれているということは、どういうことでしょう?。考えられるたった1つの答えは、お互いが定数になっているということです。つまり、右辺=定数、左辺=定数ということです。勿論2つの定数は同じになっていなければなりません。例えば定数をω2としてみます。すると、上式の右辺は以下になります。
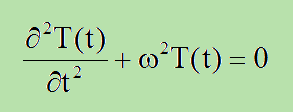
上の微分方程式の一般解はT(t)=Asin(ωt)+Bcos(ωt)で書けます。もう少し厳密に言うと、T(t)=Z1e-iωt+Z2eiωtになります。つまり、T(t)は調和関数で出来ていますので、ωは振動周波数ということになります。すると、微分方程式の左辺は以下のように書けます。
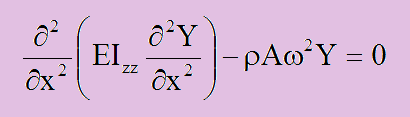
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |