4つ上の微分方程式のy(x,t)を直接Y(x)eiωtと置いても、上の式と同じ結果が得られます。音響固有値解析のところでも、突然Ψ(x,y,z,t)=ψ(x,y,z)eiωtと置いて話を進めていました。これは、変数分離の結果だったのです。
ところで、この微分方程式の一般解はどのように書けますか?。4回微分して元の関数に戻らなければなりません。考えられる関数として、sinh(βx), cosh(βx), cos(βx), sin(βx)が上げられます。4階微分の方程式ですから、境界条件も4つ必要になります。ですから、解も4つの独立関数が必要になります。関数の引数は無次元ですので、βxをλx/Lで表すことにします。ここに、Lはビーム長、λはωの関数になっている固有値で無次元です。すると、上の方程式の一般解は以下で書けることになります。
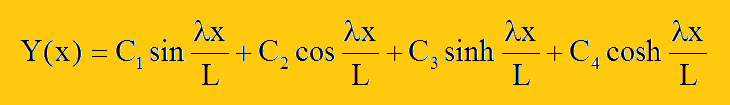
ここに、C1からC4は、境界条件で決まる値です。それから固有値のλですが、上の一般解を微分方程式に代入すると、以下を得ることができます。
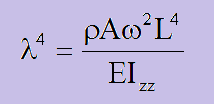
確かにλとωは従属関係にあることが上の式からわかりますね。ところで、 C1からC4を決める境界条件ですが、以下が考えられます。
| 境界条件 | 変位 | 撓み角 | モーメント | せん断 | Y | dY/dx | dY2/dx2 | dY3/dx3 |
|---|---|---|---|---|---|---|---|---|
| ヒンジorローラー | 0 | 0 | 0 | 0 | ||||
| 固定支持 | 0 | 0 | 0 | 0 | ||||
| 自由(支持なし) | 0 | 0 | 0 | 0 | ||||
| 回転拘束 | 0 | 0 | 0 | 0 |
今後の計算のためにY'(x), Y"(x), Y"'(x)を前もって計算しておくと便利です。ここに、 Y'(x)=dY/dx、Y"(x)=dY2/dx2、Y"'(x)=dY3/dx3のことです。 結果は以下のようになります。
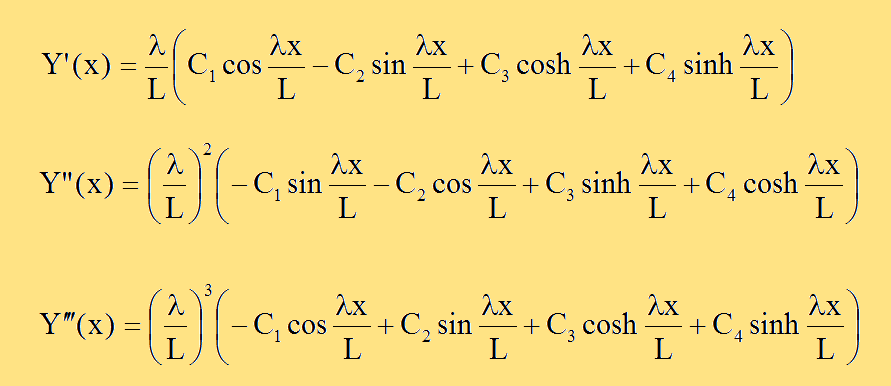
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |