それでは、早速様々なケースの梁の固有値を計算してみましょう。
■片持ち梁■
片持ち梁ですから、左端つまりx=0を固定端、x=Lを自由端とします。すると、
Y(0)=0とY'(0)=0から
0=C2+C4と0=C1+C3
が得られます。つまり、C2=-C4とC1=-C3と言うことになります。
そして、Y"(L)=0とY"'(L)=0から以下が得られます。
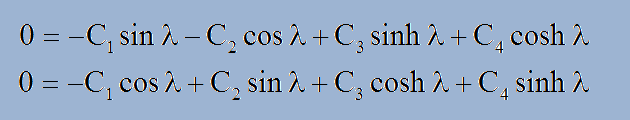
C2=-C4とC1=-C3から3と4を消去すると、 以下の結果がえられます。。
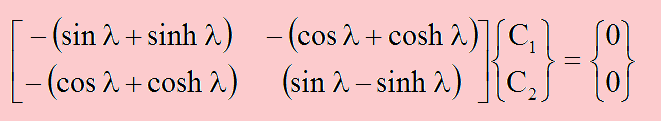
固有値λは上式を満足していなければなりません。つまり、上のマトリクスの行列式をゼロと置いたときが解になります。ここで注意したいことは、sin2(x)+cos2(x)=1 、cosh2(x)-sinh2(x)=1 です。これを踏まえると、行列式=0は以下の結果になります。
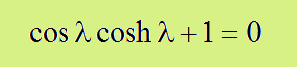
上式の厳密解は有りませんが、近似解でしたらNewton-Raphson法で計算するすることができます。実際にFINDROOT.FORを実行すると、ファイルROOT.DATを出力します。最初の4つは以下のようになっています。。
| λi | 計算値 |
|---|---|
| 1 | 1.8751040687119611 |
| 2 | 4.694091132974175 |
| 3 | 7.854757438237613 |
| 4 | 10.995540734875467 |
固有値(λ)と固有振動数(ω)とは以下の関係であることは以前伝えました。
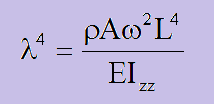
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |