これを角速度ω[radian/sec]で書くと以下になります。そして、これを周波数f[Hz]で表す場合、ω=2πfで計算できます。
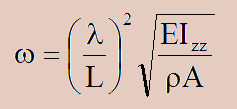 または
または
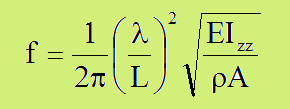
■両端自由支持(支持なし)■
この場合、両端にY"(x)=0とY"'(x)=0を与える必要があります。まず、x=0では、C2=C4とC1=C3が得られます。右端のx=Lで得られた結果にx=0での結果を代入すると、以下が得られます。
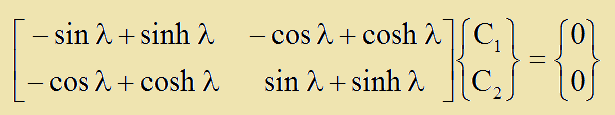
マトリクスの行列式をゼロと置くと、以下が得られます。
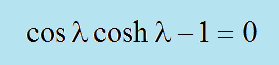
プログラムFINDROOT.FORのcosλcoshλ+1をcosλcoshλ-1に書き換え実行すると結果ROOT.DATを出力します。その一部を下に示します。
| λi | 計算値 |
|---|---|
| 1 | 4.730040744862704 |
| 2 | 7.853204624095838 |
| 3 | 10.995607838001671 |
| 4 | 14.137165491257464 |
■単純梁の場合■
1端がヒンジで他端がローラー支持の単純梁の場合、両端でY(x)=0とY"(x)=0を満足している必要があります。つまり、変位がゼロ、モーメントがゼロということです。まず、x=0の境界からみてみましょう。以下が境界条件を適用した結果です。
Y(0)=0より、 0=C2+C4
Y"(0)=0より、 0=-C2+C4
上の2式が満足できるのは、C2=C4=0になります。0=C2+C4は、C4をy、C2をxと置くと、y=-xになります。また、0=-C2+C4は、y=xです。これらの2式が交わるのはx=0のみになります。よって、C2=C4=0ということになります。次にx=Lでの境界を見てみましょう。
Y(L)=0より、0=C1sinλ+C2cosλ+C3sinhλ+C4coshλ
Y"(L)=0より、0=-C1sinλ-C2cosλ+C3sinhλ+C4coshλ
結果的に以下のマトリクス式が得られます。
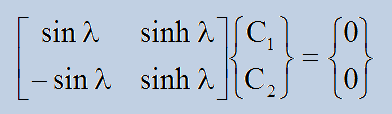
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |