上のマトリクスの行列式=0から得られるのは0=sinλsinhλです。よって、固有値はsinλ=0より以下になります。
■両端固定支持■
両端が固定の場合、両端にY(x)=0とY'(x)=0を与える必要があります。まず、x=0では、-C2=C4と-C1=C3が得られます。右端のx=Lで得られた結果にx=0での結果を代入すると、以下が得られます。両端自由と同じ結果になります。
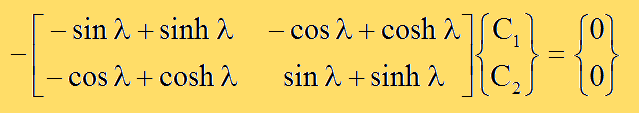
つまり、以下を解くことになります。結果はROOT.DATです。
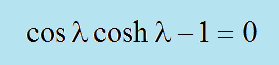
■固定とローラー支持■
左端つまりx=0を固定端とし、x=Lをローラーの単純支持とします。すると、Y(0)=0とY'(0)=0から0=C2+C4と0=C1+C3が得られます。つまり、C2=-C4とC1=-C3と言うことになります。そして、Y (L)=0とY"(L)=0から以下が得られます。
Y(L)=0より、0=C1sinλ+C2cosλ+C3sinhλ+C4coshλ
Y"(L)=0より、0=-C1sinλ-C2cosλ+C3sinhλ+C4coshλ
結果的に以下が残ります。
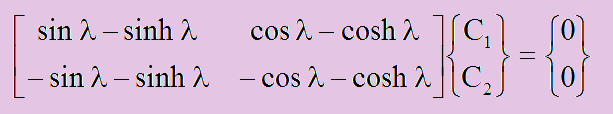
マトリクスの行列式を計算すると以下になります。
上式の両辺をcosλcoshλで割ると次の式が得られます。関数tanhλは常に正の値で、λが大きくなると急速にtanhλ=1になります。従って、固有値λ1はゼロでλnは、nπ近辺にあることになります。ここに、n>1、tanλ/tanhλのλ→0の極限は1です。
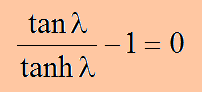
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |