貴方の疑問は、何故、”対角要素の値(絶対値)が非対角要素より小さいと良くないんですか。”だと思います。
連立方程式を快適に解くために、対角要素が強いことが条件の1つです。連立方程式を解く過程で、連立方程式の非対角要素と右辺を、対角要素で割るというステップが有ります。対角要素が弱いと、それまでに非対角要素に蓄積されている誤差を拡大することになります。
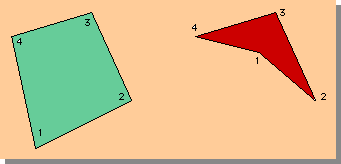
連立方程式の対角要素が弱くなるという現象は、高次要素でも起きます。下図に4-noded Isoparametric 要素を示します。左の要素は、良い結果を生みますが、右は、連立方程式の対角要素を弱くし、結果的に解析精度が悪くなります。理由は、右の要素の節点番号1において、内角が180度以上になっているからです。三角形要素の90度と同じ様な悪さをします。
■三角形要素の[N]T[N]の積分■
ここでは、[N]T[N]の積分について紹介します。1次元のHelmholtz Equation の[N]T[N]の計算で紹介した様に、有限要素式の生成項は、次の様になります。

| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |