■[K]{T}=-{Q}の{Q}の計算方法■
計算された未知数が温度{T}の場合、[K]{T}=-{Q}の{Q}は節点に集約された熱流束(Heat Flux)に
なります。この量を計算するには温度{T}が計算された後、再度[K]を計算し温度と
マトリクス演算すれば得られます。プログラム
FEM3HFLOW.FORを作成しましたので、
使ってみて下さい。NEX=2, NEY=2の場合の計算結果ファイル
SOLUTION.FEMのスクロールダウンした所にある
Q=HEATFLOWをみて下さい。
節点5は領域内の点ですのでQ=0のなっています。節点9では、y方向にQ=-0.4530818393219729になっています。
絶対値で最大は節点8でQ=-0.6407544820340814です。もっともらしい値になっていると思います。
大きいNEXとNEYで計算したとき{Q}がどうなるかチェックしてみて下さい。
■ここで紹介したプログラム■
次に進む前に、ここで使ったプログラムの紹介をおさらいしておきます。
| プログラム名 | 要素 | 簡単な説明 | 出力ファイル |
|---|---|---|---|
| FEM3.FOR | 3節点1次 | フルマトリクスで 2次元Laplace Equationを解く |
SOLUTION.FEM
SOLUTION.BIN |
| FEM3Q.FOR | 3節点1次 | バンドマトリクスで 2次元Laplace Equationを解く |
SOLUTION.FEM
SOLUTION.BIN |
| FEM3HFLOW.FOR | 3節点1次 | フルマトリクスで 2次元Laplace Equationを解き {Q}を計算する |
SOLUTION.FEM
SOLUTION.BIN |
| SETFEM3.FOR | 3節点1次 | 入力データを作成 | FEM03INPUT.DAT
PARAM.DAT ELEMENT3.OUT |
| GRA3FILE.FOR | 3節点1次 | グラフィックデータを計算 | TEMPERAT.OUT |
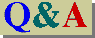 |
 |
|---|
| BACK | NEXT-Remark |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |