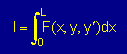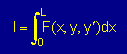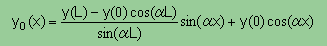One Dimensional Finite Element Method
Calculus of Variations-2
■First Variation■
もし上の 状態関数(前のページ) が単位長さ当たりのエネルギーを表しているとします。
すると領域内の全てのエネルギーを知るには、y(x) に沿って 状態関数 を積分する必要があります。
変分法ではy(x)の形を色々と変えながら状態関数 を下式によって積分し積分値が極値(最大または最小)を示す y(x) を探します。
ここでは積分値が極値(最大または最小)になる y(x)を y0(x) で表します。
後で詳しく説明しますが y0(x) は Helmholtz equation の厳密解になります。
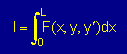ここで取り扱う問題はDirichlet 境界としたため上の様な積分式になっています。
もし Neumann 型の境界が存在すると、境界積分が上の式に追加されます。
頭がくしゃくしゃしてきますので、ここでは、ひとまずNeumann 型のことは忘れて下さいね。
ところで Helmholtz equation を y(0) と y(L) の Dirichlet 境界条件で解くと下の様になることは前に説明しましたね。
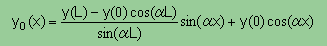上の解をその上に表示してある積分式に代入するとI0 が計算されこの値は極値(最大または最小)になっているはずです。
ところが私達が求めようとしているのは厳密解ではなく近似解(変分法では admissible solutions という｡)です。
もちろん厳密解(y0) が常に存在すれば有限要素法や変分法の勉強は必要ありませんがね。
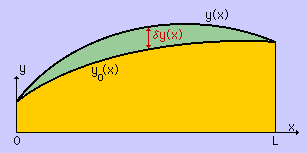
では無理矢理上の厳密解をベースに近似解を作ってみましょう。
下式がそうです。
その下の図も参考にして下さいね。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method