次に、前ページの式の右辺にDivergence の定理を施すと、領域積分を境界積分に変換出来ます。下の様になります。

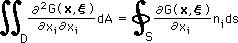これまでを総合すると、問題になっていた領域積分は、次の様に書けます。

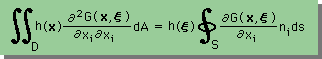
これで、Green's Second Identity の領域積分は、境界積分に変換され、下の境界積分のみを計算することで、Laplace equation を解けることになります。

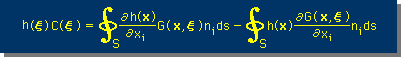
上式をLaplace equation の境界積分式(境界要素式 or Boundary Element Equation)といいます。そして、C(ξ) は、Free term と呼ばれています。これは、問題になっていた領域積分から得られた項目です。下にその詳細を示します。

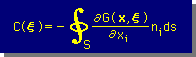
上の2つの式が境界要素法の基本式です。ここでは、Laplace equation を解く基本式を導きましたが、他の微分方程式の場合も同様な基本式が導き出されます。なお、微分方程式から境界要素法の基本式を導き出す手続きについては、のちほど詳しく説明します。