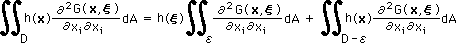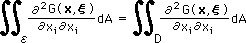■領域を２つに分割■
前ページの領域積分を評価するために、下図に示す様に領域を2つに分けます。ここで、再度、確認しておきますが、h(x) は、境界と領域内において、xとy方向に微分できる連続な関数です。つまり、ブレークや突起の無いスムーズな関数ということです。

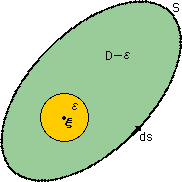
1つは、source point (ξ) を中心とする半径εの円です。これを領域εと呼ぶことにしましょう。半径εの円は、非常に小さい面積とします。針の先ほどの面積だと思って下さい。つまり、h(ξ) は、半径εの円において一定な値になっていると考えてよいことになります。結果的に、一定なh(ξ) は、積分の外に出すことができます。

もう1つは、source point (ξ) を含まないその他の領域(D-ε)です。この領域では、L(G(x,ξ)) =0 ですから、積分結果もゼロになります。

すると、前ページの領域積分は、次の様に書けます。

右辺の第2項目は、上で説明したように積分結果はゼロです。そして、右辺の第1項目の積分範囲は、εですが、領域 (D-ε) の部分の L(G(x,ξ)) =0 を加えても結果は、変わりません。よって、h(x)=一定を考慮すると、下のことが言えます。