ここで、もう1つ新しい変数を紹介します。下をみて下さい。Kernel function の微分です。丁度、有限要素法の∂δu/∂x_i に似ていますね。

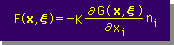
上の式には、係数Kが掛算されていますが、これは、Kernel function の分母にある同じKとでキャンセルされます。そして、上の変数を使って積分式を書き替えると、次の様になることは前に説明しました。

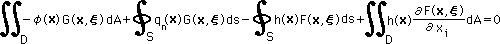上式の左辺の右端の領域積分ですが、δ(x,ξ) の特性から、次の様な関係式が得られます。これについても既に説明済です。

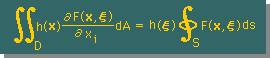
■Bounady Element Equation for Laplace Eq.■
上の関係式を積分式に代入すると、Laplace 方程式(正確にはPoisson 方程式) の境界要素式が得られます。下にその境界要素式を示します。

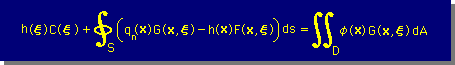
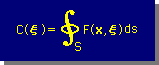
上の式のφ(x)＝0 で K=1 とすると、上の結果は、Fundamentals で紹介した式と同じになります。