変数が、要素上で一定であるため、変数(h(x) 及び q_n(x))の離散化に形状関数を使う必要がなくなりました。h_j 及び q_nj は、要素の中央での温度と放線方向の熱流束になります。

上の式で、計算が必要になるのは、下の2つ積分のみです。これらの積分は、数値計算でなく厳密に計算できます。厳密計算については、境界要素法の書物を参考にしてください。ここでは、有限要素法で親しんできたGauss-Legendre Quadrature で積分を行うことにします。

ここに、index i が Source point が存在している節点番号です。そして、index j が要素番号を意味します。また、 Source point でないその他の節点を Observation point と言います。例えば、 Source point が節点番号の1にあった場合、1以外の全ての節点を Observation point と言います。

Source point を節点1から順に節点nまで全ての節点に置き、上の式の計算を行うと、全てのSource point 対応したG_ijとF_ijを計算することができます。つまり、マトリックス[G]と[F]が出来上がります。Cの計算もこの時点で行います。この時点では、実際どの様に計算するかは分からなくて良いです。計算のイメージがつかめればOKです。

■マトリックス式■
これまでの、作業をマトリックス式に書き表わすと下の様になります。マトリックス[C]=[C_ij]は、対角要素のみに数値があり、非対角要素はゼロになっています。つまり、C_i=[C_ii]です。 ここに、[G]=[G_ij]、[F]=[F_ij] とします。そして、マトリックス[C],[G],[F]のサイズは、nXnになっています。nは、節点の数です。一定要素の場合、節点数と要素数は同じです。

有限要素法で紹介しましたように、[K]マトリックスの対角要素は、非対角要素の合計を負にした値と同じでした。 有限要素法で学んだ特徴を参照して下さい。 境界要素法でも同じことが言えます。 上式の[F]と[C]を合体させたマトリックスを[F]とし、{q_n}={0} そして{h}={1}とすると、下の条件が得られます。
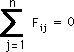