■例題2-2: A_z=一定を境界条件としてB(x)を得る方法■
例題1の結果から、導線の周囲のA_z値は、大きく変動せず0.25～0.3の範囲でした。 そこで導線の周囲のA_z値を一定の値と仮定して磁束密度B(x)を計算します。そして計算結果と下のAmpere's Lawで電流Iは簡単に計算できます。

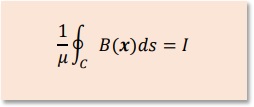
電流がI=1[A]のとき磁束ΦはA_zの2倍でした。つまり、磁束ΦはΦ=2×A_zです。 ですから繰り返し計算で電流Iが1[A]になるAz値を探せばよいことになります。 実際の計算ではμ₀=1を使い、境界条件として下図に示す様にA_z=0.5を上側の導線に与え、 他方の導線には、A_z=-0.5を与えてあります。

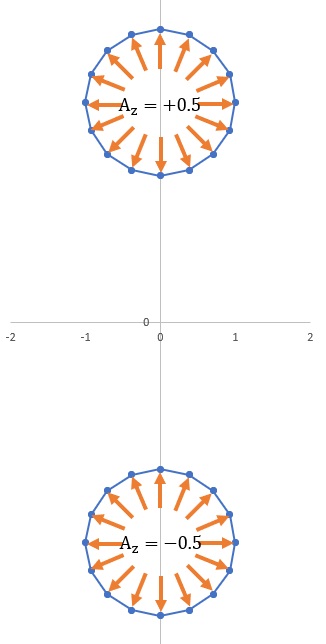
計算されたB(x)から電流Iを計算しその逆数(1/I)が電流I=1[A]の時の磁束になります。 微分方程式が非線形ですと、A_zを変えながらIがI=1[A]になるまで繰り返し計算になります。 しかし、今回解いているラプラス方程式は線形ですので、1/Iが求めるA_zになります。 もう少し説明を加えると、最初に計算された値をΦ₁とI₁とします。Φ₁=2×A_zですからΦ₁=1です。 また、Φ₁=LI₁ですから、L=Φ₁/I₁です。 A_zを変えて2回目を計算したとします。すると、Φ₂=LI₂です。この時I₂=1が得られたとします。 Lは同じですから、以下が言えます。Φ₁=1、I₂=1です。

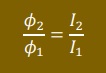
よって、Φ₂=1/ I₁となります。ラプラス方程式は線形ですか繰り返しは１回で済みます。
今回は、この問題のためにデータ作成プログラムを新たに作成しました。 それは SETUAZ.FOR です。このプログラムを実行すると、既知の境界値としてA_zを指定できます。 境界要素法のプログラムは、以前と同じです。 次に、計算結果の読み取りを容易にするために、プログラム POSTPROCESS.FOR には、上に示すB(x)の線積分を計算する部分があります。 結果はファイル DELTAP.SOL に入ります。