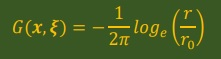
積分式にGreen関数を代入すると以下になります。

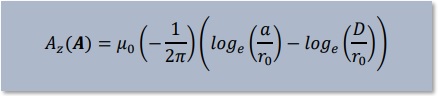
ちょっと整理すると見慣れた下式が出来ました。 線上(x,y=0)では、log((D/2)/(D/2))ですからA_zの値はゼロです。

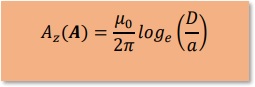
磁束Φは、上の式の2倍ですから、以下の結果が得られることになります。ここでは、f₁と呼ぶことにします。

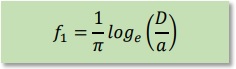
上の式は、電磁気学の書物等でインダクタンスの近似式でよく見かけます。 この式を幾何学的に理解するならば、電流を導線の中心に集中させ上の図の点 A とA' で得られた 磁気ベクトルポテンシャルの値から磁束を計算していることになります。 上の議論を点ξ=Bについて行うと以下になります。 点Bからx₂までの距離はD-aですから、(D-a)/a=(D/a)-1になります。

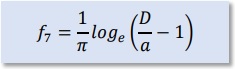
この場合、２つの導線が接触するとD-a=aですから、磁束はゼロになります。 同様に点ξ=Cについて行うと以下の結果になります。ここではf₂と呼ぶことにします。

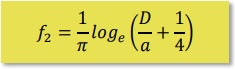
ラプラス方程式のGreen関数(カーネル関数)を使うとわりと簡単に磁束の近似式を導くことが出きます。