■導線表面で電位(V)一定で得られた結果と関数f3の関係■
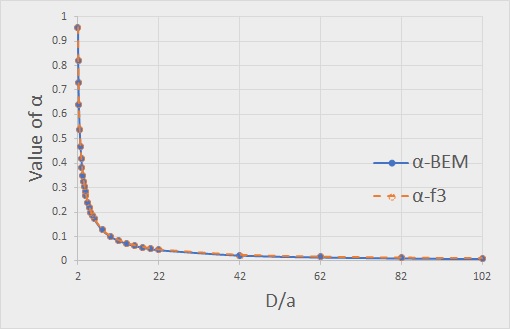
これまでに何回も触れてきましたが、BEM解析で導線表面の電位(V)を一定として得られた結果は、関数関数f3とほぼ 同じでした。 ここでもう少し話を展開してみます。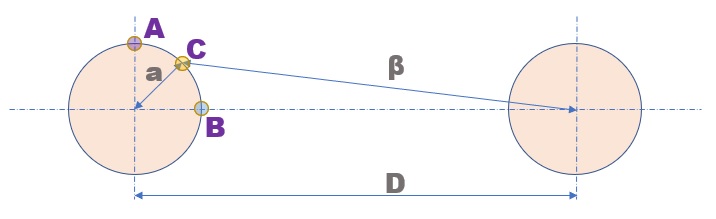
| \begin{eqnarray} f_1=\frac{1}{\pi}{log}_e\left(\frac{D-\alpha a}{a}\right) \end{eqnarray} |
| \begin{eqnarray} α_{f_3}=\frac{D}{2a}-\sqrt{\left(\frac{D}{2a}\right)^2-1} \end{eqnarray} | \begin{eqnarray} α_{BEM}=\frac{D}{a}-{exp}\left(πf_{BEM}\right) \end{eqnarray} |