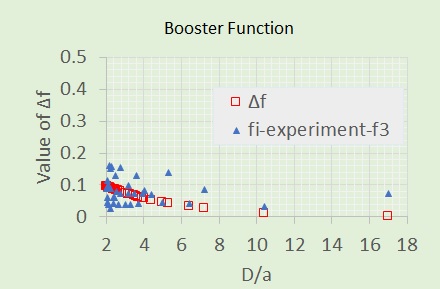
そしてこのΔfをf3に加算しプロットすると下図左の□ようになります。 青の▲は、実験値です。 橙の●は、f3です。 そして横軸のD/aを2から6の区間をプロットすると以下の右になります。
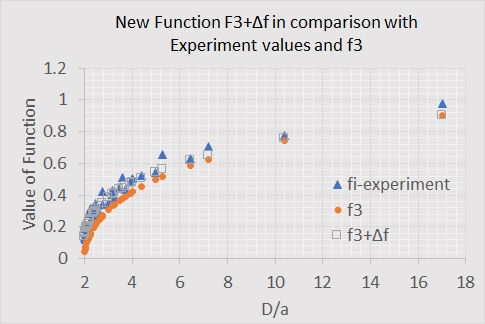
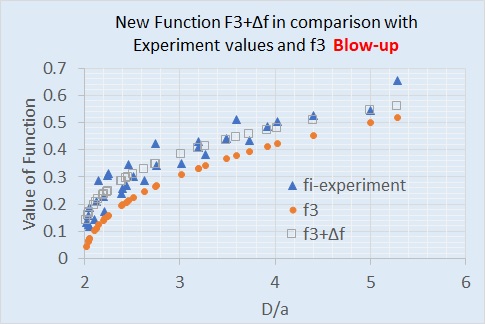
なんとなくいい感じのL関数の近似式になっています。したがって、インダクタンスの関数は以下の式で表すことができます。
| \begin{eqnarray} f_{new}=\frac{1}{\pi}\left(0.3{exp}\left(-0.25\left(\frac{D}{2a}-1\right)\right)+ {log}_e\left(\frac{D}{2a}+\sqrt{ \left(\frac{D}{2a}-1\right) \left(\frac{D}{2a}+1\right) } \right)\right) \end{eqnarray} |
| \begin{eqnarray} f_{new}(r)=\frac{1}{\pi}\left(0.3{exp}\left(-0.25\left(\frac{r}{2}-1\right)\right)+ {log}_e\left(\frac{r}{2}+\sqrt{ \left(\frac{r}{2}-1\right) \left(\frac{r}{2}+1\right) } \right)\right) \end{eqnarray} |