Electromagnetics and Ham Radio
Experiment 5
Lの関数値がCの関数値よりどれくらい離れているかは下図のLC/(με)のグラフで分かります。グラフからは、少なくとも以下の2件が読み取れます。

D/aが2から6の範囲で関数値の差が大きい
関数値は導体の形態の違いに差がある

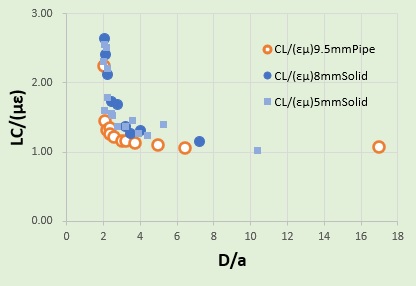
つまり、LとCそれぞれに関数が必要と思われる。そして、パイプはソリッドと比較しよりLC/(με)が１に近くなっています。

書物やネットで見られるように、Lの関数値とCの関数値が同じであれば、全ての計測値がLC/(με)=1の線上に来るはずです。 グラフをよく見るとD/aの極限値の2近傍では、LC/(με)が1以上の大きな値を示しています。 このことからLの値はCの関数で置き換えられないことが分かります。ただし、D/aが6以上であれば問題なさそうです。 この場合特性インピーダンスは、D/aが十分大きいと仮定すると Z0=120*loge(6)=215Ωになります。 (D/aが大きいと関数fiが違っても値はほぼ同じになる) Balunを正しく作るには、特性インピーダンスの値が50から100Ωの範囲をできるだけ正確に算出できる計算式が必要になってきますので、 Lの関数は、Cの関数で置き換えられないということになります。つまり、

D/aの値 関数の条件
2～6 Lの関数値 ≠ Cの関数値
6以上 Lの関数値 = Cの関数値

Preceding Page Next Page
Menu Inductance Capacitance Z0 EXP Balun Coaxial Off center fed DP Helmholtz FEM BEM
Internet College of Finite Element Method