■計算例その2■
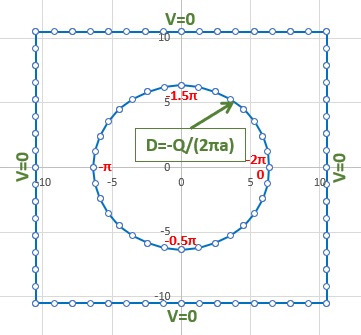
上の条件に満足すると思われるチューブの組み合わせを計算で探し出してみましょう。 当たりを付けるために同軸ケーブルの式Z₀=60×loge(b/a)で計算してみます。 また、境界要素法で得られた計算結果V(a)からは、Z₀=2×π×60×V(a)で特性インピーダンスが得られます(π=3.14159....)。 計算例では、D=25mm、t=2mm、d=12.7mmを選んでみました。 上図にしめすaとbは、a=6.35、b=10.5になります。
下図に2次要素による要素分割と境界条件を示します。 角パイプの部分は32要素で、丸パイプの部分は、16要素で分割してあります。 境界条件ですが、角パイプの部分は、Dirichlet型で値はV=0です。 丸パイプの部分は、Neumann型で値は、D=-Q/(2πa)=-0.02506377です(π=3.14159...のパイです)。 Dの符号ですがベクトルの方向が領域に向かっていますので負になります。
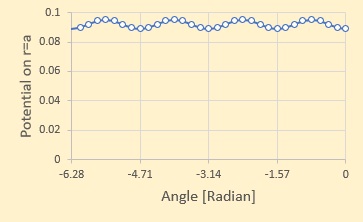
まずデータ作成プログラム SETCOAXIAL-OUTER-SQUARE.FOR を実行すると、ファイル BOUNDARY.DAT と入力データ BEM2.DAT を作成します。 次に2次要素の境界要素法の解析プログラムBEM8QUDQ.FORを実行すると、結果ファイル BEM2.SOL を出力します。その他ファイルECHOPRT.SOLも出力します。これは、入力データを 読み易くするためのファイルです。計算結果に不道理な箇所があったときに、 入力データをチェックできます。