■境界要素法の2次要素による同軸ケーブルの解析■
ペア導線の解析では1次要素の境界要素法を紹介しましたが、ここでは2次要素を用いた境界要素法を活用し同軸ケーブルの解析を行ってみます。
2次要素の境界要素法の詳細については、
BEM
のページを見て下さい。
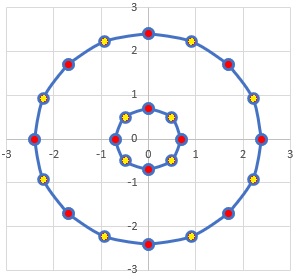
まず、下図の領域の要素分割を見て下さい。データは、上のグラフと同じ
5D-2V
のa=0.7, b=2.4, ε=1, Q=1です。
内側の円と外側の円の間には絶縁体が入ります。
計算を実施するには、まずプログラム
SETCOAXIAL-NEUMANN.FOR
を実行すると、下図を描くデータ
BOUNDARY.DAT-ELEMENT0408
と2次要素の境界要素法のプログラム
BEM8QUDQ.FOR
用の入力データ
BEM2.DAT-ELEMENT0408
を作成してくれます。
BOUNDARY.DAT-ELEMENT0408
は表計算ソフトに読みこかせると作図してくれます。
最後に2次要素の境界要素法の解析プログラムBEM8QUDQ.FORを実行すると、
結果ファイル
BEM2.SOL-ELEMENT0408
を出力します。BEM8QUDQ.FORのexeファイルは無料で提供します。
| 内円の 要素数 | 外円の 要素数 | 全体の 要素数 | V(a) | Ve(a)厳密解 | 誤差 |V(a)-Ve(a)|/Ve(a) |
|---|---|---|---|---|---|
| 4 | 8 | 12 | 0.195565728 | 0.196101757 | 0.002733425 |
| 8 | 16 | 24 | 0.196039328 | 0.000318351 | |
| 16 | 32 | 48 | 0.196087826 | 7.10424E-05 | |
| 32 | 64 | 96 | 0.196095981 | 2.94566E-05 | |
| 64 | 128 | 192 | 0.196098945 | 1.43442E-05 | |
| 128 | 256 | 384 | 0.196100356 | 7.14906E-06 |