Electromagnetics and Ham Radio
Coaxial10

2次要素の境界要素法(2D-BEM-Parabolic Element 0408)でも同じ条件で計算を行いました。 この BEM については後ほど詳細を紹介します。
それから厳密解(Exact Sol)も図に表示してあります。 厳密解は、以下の式で計算しています。

\begin{eqnarray} V(r)=\frac{1}{2\pi}{log}_e\left(\frac{b}{r}\right) \end{eqnarray}

下表は、上記４ケースの計算条件と結果を示しています。

ケース	r=0での 境界条件と 境界値	r=aでの 境界条件と 境界値	r=bでの 境界条件と 境界値	結果
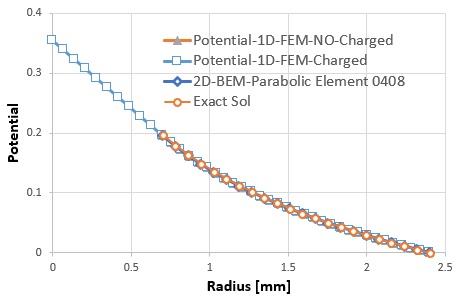
1次元FEM 分布電荷	Neumann 値=0		Dirichlet 値=0	Potential-1D-FEM-Charged
1次元FEM Neumann境界		Neumann 値=-0.1114	Dirichlet 値=0	Potential-1D-FEM-NO-Charged
2次元BEM Neumann境界		Neumann 値=-0.22736	Dirichlet 値=0	2D-BEM-Parabolic Element 0408
厳密解		Neumann 値=-0.22736	Dirichlet 値=0	Exact Sol

下のグラフの計算結果を見て下さい。４つのケースの誤差ですが、 r=aからr=bまでの計算結果の最大差(厳密解との比較)は0.2%以内でほぼ同じでした。 ちなみにr=aでの値はV(a)=0.195916です。 そこで、比誘電率ε_r=2.2とV(a)=0.195916とで特性インピーダンスを計算すると、 Z₀=49.84Ωになります。

\begin{eqnarray} Z_0=60\frac{2\pi}{\sqrt{\varepsilon_r}}V(a)=49.84\ [\Omega] \end{eqnarray}

---

Preceding Page Next Page

---

Menu Inductance Capacitance Z₀ Exp Balun Coaxial Off center fed DP Helmholtz FEM BEM Internet College of Finite Element Method