■例題の計算領域■
静電容量の計算方法を示すために実際的な例題を取り上げます。 下図は、無限長のペア導体の単位長さを切り取った状態です。上の導体に+Q、下の導体に-Qの電荷が与えられています。 ペア導体の中心線間の距離はDで、導体の半径はaです。

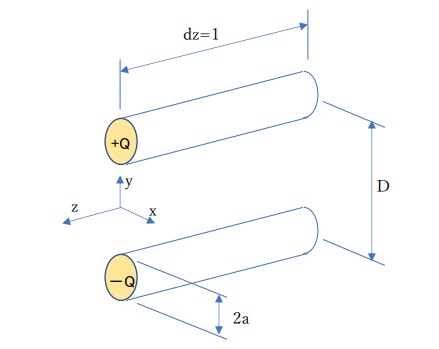
電界はx-y面の2次元に現れ、z軸のどこを切っても同じ電界の景色になります。 便宜上、誘電率はε=1とします。電荷の値は、これも便宜上Q=1[C]としておきます。

■2次元空間での方程式と静電容量の計算方法■
これまでに導いた式は、3次元でした。２次元の場合でも本質的には、全く同じですが、下に示す様に積分記号が変わります。 まず、ガウスの定理(Gauss's Law)は、以下になります。