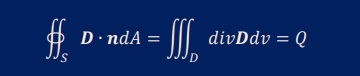| \begin{eqnarray} \vm{D}=\varepsilon\vm{E}=\varepsilon_r\varepsilon_0\vm{E} \end{eqnarray} |
| \begin{eqnarray} D_i=-\varepsilon\frac{\partial V}{\partial x_i} \end{eqnarray} |
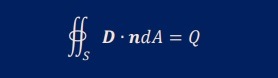
かなりすっきりした式になりました。 ここまで来ると後は様々な定理で式を展開できるようになります。 積分される項目がX・tだとストークスの定理がつかえます。そしてX・nだと発散の定理が使えます。 上の式に発散の定理を適用すると、以下になります。