
すると電界Eについて、電位の差分ΔV=V2-V1は、ΔV=-ExΔxで得られると定義されています。
そしてΔx→zeroの極限をとり、この電位差と電界の関係を拡張すると、以下の様に書けます。
| \begin{eqnarray} \vm{E}=-\left(\frac{\partial V}{\partial x}\vm{i}+\frac{\partial V}{\partial y}\vm{j}+\frac{\partial V}{\partial z}\vm{k}\right) \end{eqnarray} |
■静電場に関する理論■
ガウスの定理(Gauss's Law)によると、電界Eと電荷Qには次の関係があります。
式中のε0は、電界が存在している領域が真空のときの誘電率です。
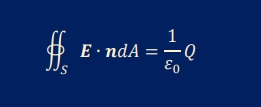
電荷Qを含む体積の表面から出てくる電界Eは、
電荷Qを誘電率ε0で割った値に等しい。
単位法線ベクトルのnは表面に対し外向きになっています。
電界は様々な誘電体でも存在します。
しかし、電界に誘電体を置くと分極(polarization)が起き、
誘電体の内部では電荷が打ち消し合い誘電体の表面(電界の入り口と出口)に電荷が存在するようになります。
結果、誘電体の内部のみ電界が弱くなるという現象がおきます。つまり、2つの電界が存在することになります。