Electromagnetics and Ham Radio
Capacitance26
今回は境界での電位Vが一定ですから、線積分から電荷Qを求めます。ファイル
DELTAP.SOL
を見て下さい。
積分結果Q= 1.7756268695206572となっています。
電荷がQ=1になるように電位Vを決定すればよいことになります。
解きている方程式は線形ですので、2V/Q=2×0.5/1.7756268695206572=0.563181385214が求める電位差になります。
Gauss's Lawで導線表面の電束密度D(x)を計算し、
計算されたD(x)と比較してみます。
D(x)はファイル
BOUNDARY.SOL
に入っています。以下がその結果のグラフです。
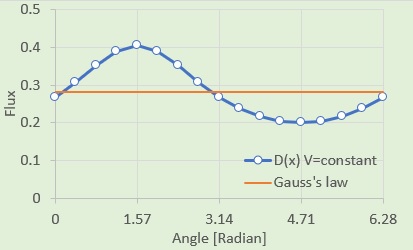
Gauss's Lawの値が
BOUNDARY.SOLからの
D(x)のほぼ真ん中を貫いています。
Gauss's Lawでの値が0.2826で、計算結果D(x)の平均値が0.2844です。
良い結果になっています。
次に、RADIUS=0.5を使って2つの導線間の距離Dを変化させたときの電位差δVの計算を実行してみました。以下がその結果です。
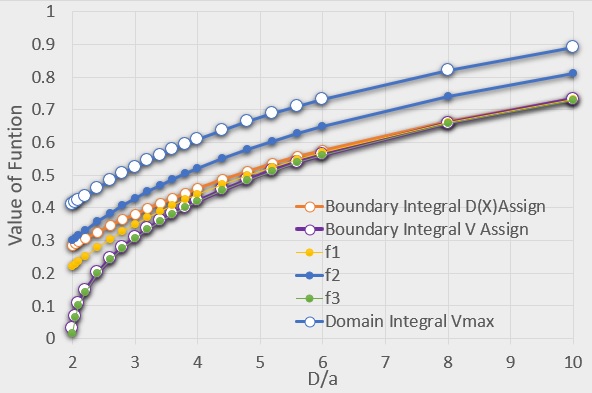
図のBoundary Integral V Assignが今回の結果です。
横軸はD/aです。
図を見ると今回の結果は、書物でみる下式のf3と良好な相関で一致しています。
|
\begin{eqnarray}
f_3=\frac{1}{\pi}{log}_e\left(\frac{D+\sqrt{D^2-4a^2}}{2a}\right)
\end{eqnarray}
|
Preceding Page
Next Page
Menu
Inductance
Capacitance
Z0
Exp
Balun
Coaxial
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method