Electromagnetics and Ham Radio
Capacitance25
もう少し説明を加えると、最初に計算された値をδV1とQ1とします。
δV1=2×VですからδV1=1です。
また、CδV1=Q1ですから、C=Q1/δV1です。
境界条件の電位Vを変えて2回目を計算したとします。
すると、CδV2=Q2です。この時Q2=1が得られたとします。
キャパシタンスのCは同じですから、以下が言えます。
δV1=1、Q2=1です。
|
\begin{eqnarray}
\frac{Q_1}{{\delta V}_1}=\frac{Q_2}{{\delta V}_2}
\end{eqnarray}
|
よって、δV2=1/Q1となります。ラプラス方程式は線形ですか繰り返しは１回で済みます。
今回は、この項のためにデータ作成プログラムを新たに作成しました。
それはSETUAZ.FORです。
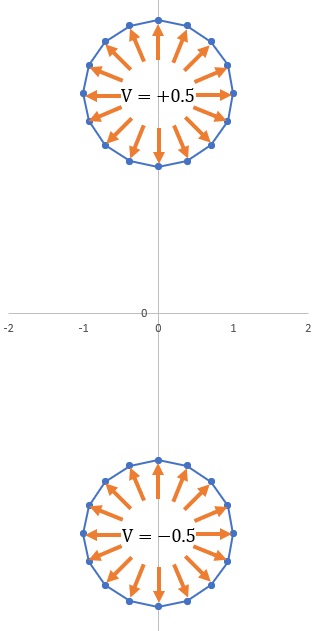
このプログラムを実行すると、既知の境界値としてVを指定できます。境界要素法のプログラムは、以前と同じです。
次に、計算結果の読み取りを容易にするために、プログラム
POSTPROCESS.FOR
には、上に示すD(x)の線積分を計算する部分があります。
結果はファイル
DELTAP.SOL
に入ります。
まず、
SETUAZ.FOR
をGAP=4で実行します。RADIUS=1になっています。次に
BEM8LINU.FOR
を実行します。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Z0
Exp
Balun
Coaxial
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method