Capacitance24

Electromagnetics and Ham Radio
Capacitance24

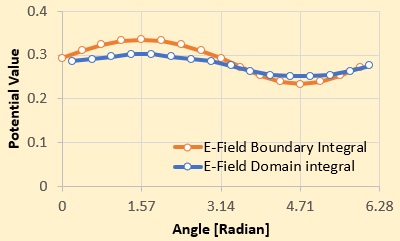
下図に上側の導線の表面の電位をプロットしてみました。Domain-Integral Vmaxが等分布電荷を与えた場合で、 Boundary-Integral D(x) Assign が導線表面にD_n(x)を与えた場合です。両者に多少の違いがみられますが、これは等分布電荷(例題１)の場合、導線の表面では電束密度D_nが出来上がっていないため導線近傍ではそれが電位に反映されていないのだと考えられます。導線の表面から少し離れた円周上で比較すると、両者の結果はかなり近くなっているはずです。

■例題2-2: 電位V=一定を境界条件としてD(x)を得る方法■
例題1の結果から、導線の周囲のV値は、大きく変動せず0.25～0.3の範囲でした。そこで導線の表面のV値を一定の値と仮定して電束密度D(x)を計算します。そして計算結果と下のGauss's Lawから電荷Qは簡単に計算できます。よって、Q=1[C]になる電位Vを計算するのは難しいことではありません。

\begin{eqnarray} \oint_{S}{\vm{D}\bullet\vm{n}ds}=Q \end{eqnarray}

電荷がQ=1[C]のとき電位差はVの2倍でした。ですから繰り返し計算で電荷Qが1[C]になる電位差(δV)を探せばよいことになります。電位差(δV)は、上側の導線表面の電位と下側の導線表面の電位の差です。話を明確にするためδVという記号を使っています。
実際の計算では、ε=1としました。また下図に示す様にV=0.5を上側の導線に与え、他方の導線には、V=-0.5を与えてあります。計算されたD(x)から電荷Qを計算しその逆数(1/Q)が電荷Q=1[C]の時の電位差(δV)になります。微分方程式が非線形ですと、境界でのVを変えながらQ=1[C]になるまで繰り返し計算になります。しかし、今回解いているラプラス方程式は線形ですので、1/Qが求める電位Vになります。

Preceding Page Next Page

Menu Inductance Capacitance Z₀ Exp Balun Coaxial Off center fed DP Helmholtz FEM BEM Internet College of Finite Element Method