| \begin{eqnarray} f_{Pmax}=\frac{1}{\pi}{log}_e\left(1.6208\left(\frac{D}{a}\right)+0.3083\right) \end{eqnarray} |
| \begin{eqnarray} f_{\partial A}=\frac{1}{\pi}{log}_e\left(0.9649\left(\frac{D}{a}\right)+0.4129\right) \end{eqnarray} |
■両計算方法による結果の比較■
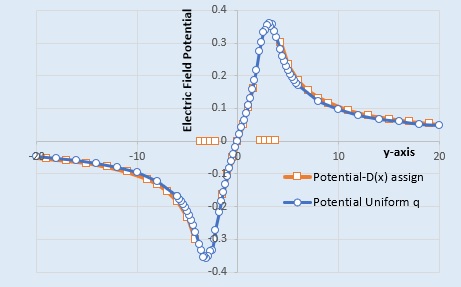
例題1と例題2の計算結果をInternal Points について比較してみました。下図を見て下さい。
導線の周りの電束密度をGauss's Lawで一定としても、例題1の電荷を等分布としたときの結果とさほど大きく違いにはなっていません。
また、上の導線と下の導線との間(y=-2~+2)の電位は、両者ともほぼ同値になっています。