■例題2-1: D_nを境界条件として電位Vを計算する方法■
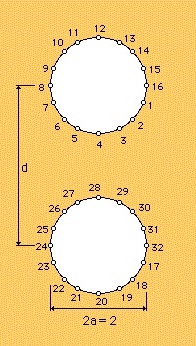
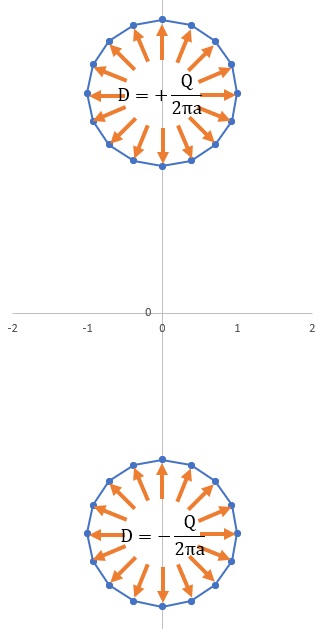
今度は、導線に電荷を与えるのでなく、それ相当の電束密度D_nをGauss's Lawにしたがって、導線の周りに一定の値を与えたらどうなるか計算してみます。上の計算結果から導線の表面の電束密度は、一定でないことが分かっていますので、ここでの計算手法は近似解ということになります。 まず、計算式ですが、以下になります。 導線の表面に電束密度を境界条件として与えるので導線内の領域積分は不要になります。 ここで注意してほしいことは、導線部分の面積は、計算領域外になります。