更に、τ_ji=τ_ij ですから、次式も正しいことになります。

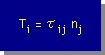
このSurface tractionと応力との関係式を Cauchy's formula と言います。そして、この Cauchy's formula を力のバランスの式に代入すると、次の様になります。

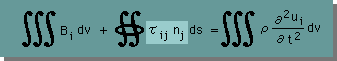
さらに、上式の面積分(Surface integral)に対し、前に学んだDivergenceの定理を応用すると、面積分を体積積分に変換することが出来ます。つまり、以下の様になります。

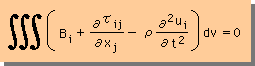
積分の範囲は、任意であるから、積分される内容もゼロになることになります。そして、Index notation の代わりに通常のxyz座標を用いて上式を書くと次の様になります。

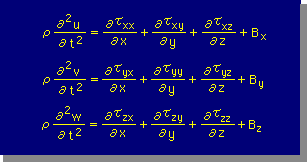
これを、Navierの式と言います。また、これは、弾性解析の支配方程式でもあります。