全ての材料において、大なり小なり、下図に示す様な応力-ひずみ曲線を描きます。つまり、力Fをかけた時と戻した時での応力-ひずみ曲線が異なることを示しています。
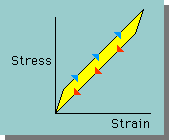
応力-ひずみ曲線とひずみ軸との間の面積は、材料に与えたまたは部材から得られるエネルギー(仕事)を意味しているので(詳細についてはのち程説明)、図の黄色の部分は、エネルギー損失を表していることになります。このエネルギー損失は、熱として空間へ放出されます。つまり、部材にエネルギーを入力しても、部材の他端からは入力されたエネルギーの100%は引き出せないことになります。逆に、このエネルギー損失が大きい材料は、振動を吸収するダンパーに使えることになりますね。
■Poisson's effect■
金属の棒を引っ張ると、引っ張られた方向へは伸びるが、その方向と直角の方向は、下図に示す様に縮むことが知られています。これを、Poisson's effectと言います。
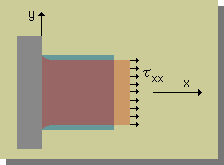
上図の場合、y方向とz方向のStrain は、次の式で表すことができます。
| εyy= - νεxx | εzz= - νεxx |
ここに、ν= Poisson's ratio と言う。
材料の力学特性を定義するためには、最低このPoisson's ratio と Young's modulus が必要になります。もっと正確に言うと、等方性材料の力学特性を定義するためには、2つの独立した定数が必要になるのです。この議論については、ReferencesのMalvernを読んで下さい。
また、Poisson's ratio は、材料の圧縮性のパラメーターとして考えることもできます。後程、詳しく触れますが、非圧縮性材料の場合、Poisson's ratioは、0.5 になります。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |