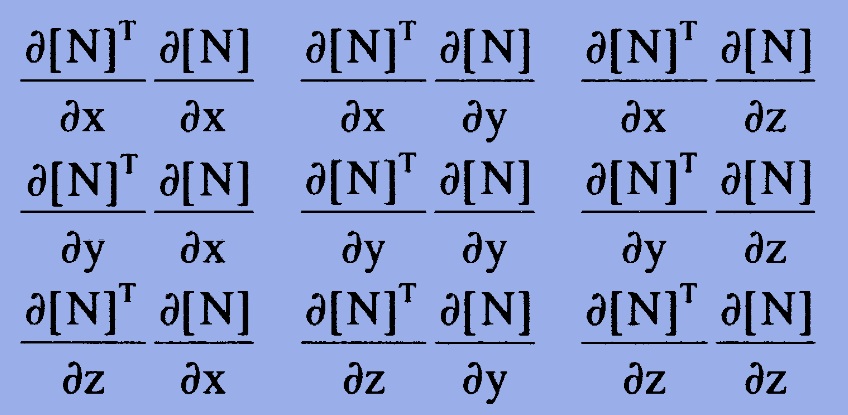
プログラムでは、要素毎にJacobianマトリクスとGauss-Legendre Quadratureを使って以下の積分を計算しておきます。

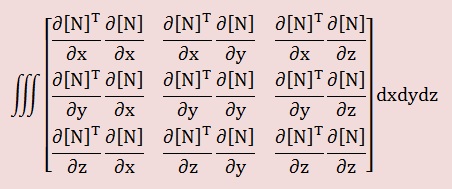
上の計算ですが、プログラムでは以下に示す四次元変数で表すと便利です。

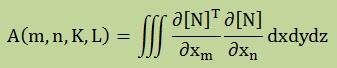
インデックスのKとLは、[N]^T[N]から出来るマトリクスのK行L列を意味します。インデックスmとnは実座標の独立変数を意味します。例えば、m=1ではx_m=x, m=2ではx_m=y, m=3ではx_m=z になります。すると、要素毎の剛性マトリクス[k]は、以下のように書けます。

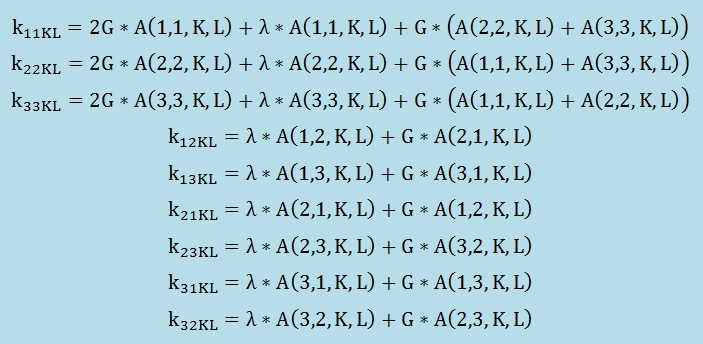
また、A_mm=A(1,1,K,L)+A(2,2,K,L)+A(3,3,K,L)とおくと、要素毎の剛性マトリクス[k]の対角要素は、以下のように簡素化されます。