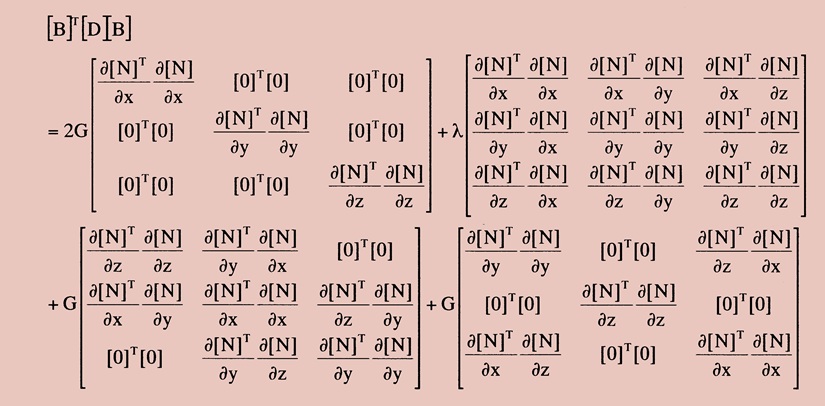
上式右辺の第1の2G項は鉛直応力、第2のλ項は膨張収縮、そして第3と4のG項がせん断応力に該当します。したがって、せん断応力の部分低減精度積分法の場合は、第3と4のG項のみを低減精度で積分します。参考までに、流体では圧力に密接に関係している第2のλ項を低減精度で積分します。以下に積分の方法と名称を書いておきます。
| 積分方法の 名称 |
2G項の 積分点数 |
G項の 積分点数 |
λ項の 積分点数 |
積分方法 |
|---|---|---|---|---|
| 正規積分法 | n | n | n | GL |
| Galerkin提案の低減精度積分 | n | n-1 | n | GL |
| 流体のPenalty法 | n | n | n-1 | GL |
| Free Selection法 | n | n | n | non-GL |
上表のGSとはGauss-Legendre quadrature積分方法のことです。正規積分法とは、積分される関数を厳密に積分できるサンプリング点数のことです。例えば、関数が3次式の場合はサンプリング点が3のGLを使えば厳密解が得られます。Free Selection法において、サンプリング点数はGL法と同じですが、座標値が違います。例えば2点のGL法では、座標値ξ=+/-0.577350269を使いますが、Free Selection法ではそれ以外の座標値を使います。弾性解析では剛性マトリクスが法線微分とクロス微分から成っています。このクロス微分は数値的に剛性を高める役目をしているためShear Lockingと言う現象を起こしてしまいます。ですから要素内の積分を精度良く計算できたからといって最終計算結果が良いとは限りません。何故かというと有限要素法は計算精度を積分だけでなく要素のAssemblyに依存しているからです。Assemblyが高剛性の一因になっています。それを緩和するため、積分点の座標を少し要素の中心に移動すると、Shear Lockingが収まり数値的な剛性が弱くなります。
少し脱線しました。話を元に戻します。上の式を観察すると、以下を前もって計算しておくと便利であることが分かります。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |