■剛性マトリクスのプログラミング■
この剛性マトリクスですが、いざプログラムに書き下ろそうとすると、ちょっと大変であることが分かります。しかし、手順を踏まえれば問題なくプログラミングできます。そこでここでは、その計算手順とグローバル剛性マトリクス[K]に足し込む操作(assembly)を紹介します。まず行われなければならないのが[B]T[D][B]の展開です。ここでは、要素単位の剛性マトリクスを[k]=[B]T[D][B]で表すことにします。すると、[k]は、3次元8節点要素の場合24×24のサイズになります。展開の前に準備しておかなければならないのが、以下の形状関数の微分です。
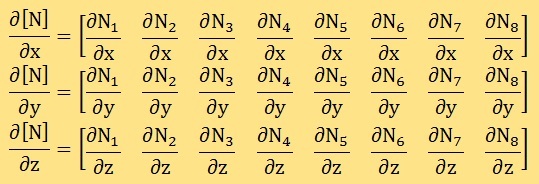
Iso-Parametric要素のところでも説明しましたが、形状関数[N]は無次元座標(要素座標)の独立変数(ξ,η,ζ)での微分は簡単にできますが、x, y, zでの微分を得るにはJacobianマトリクスを準備しておく必要があります。つまり、与えられたξ,η,ζ点において[N]のx,y,zでの微分を得るには、以下の連立方程式を解く必要があります。
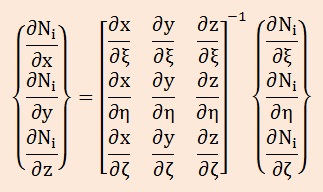
形状関数の微分の計算方法が分かったところで、[k]=[B]T[D][B]の展開を行ってみましょう。以下の[D]には、等方性材料が考慮されています。
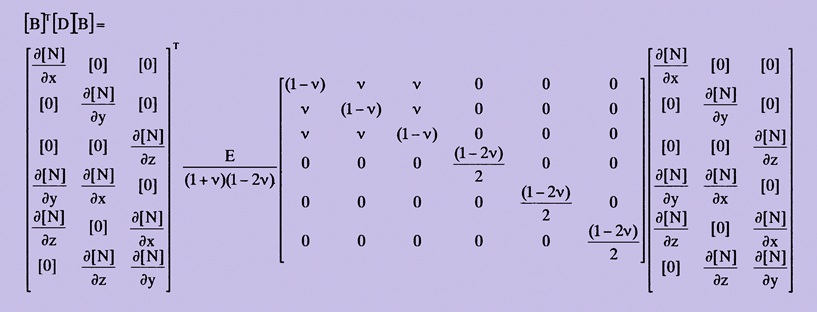
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |