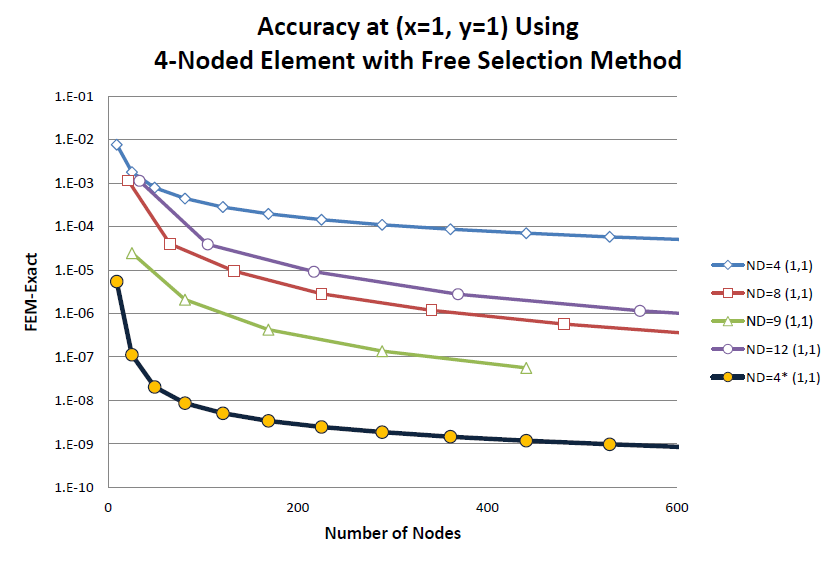
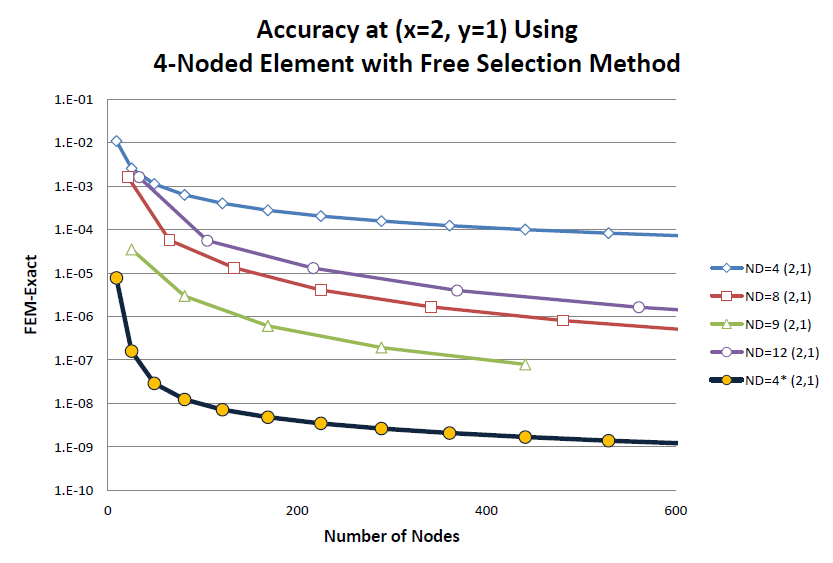
パラメトリック要素中で一番精度の悪い要素でしたが、積分ルールを変えるだけで最も精度の良い要素になってしまいました。ここで問題になるのがサンプリング点の座標の決め方です。ソリッドの場合、要素のアスペクト比に左右されことが分かっています。ポテンシャル問題の場合は今後研究を重ねて行きたいと考えています。1つ言えることは、ξを0.8163から0.8165の範囲にとることで、要素分割数と要素のアスペクト比(1から10)に関係無く高い精度の計算結果が得られました。アスペクト比が3でもξ=0.8165を使うと9節点2次要素並みの計算精度が得られました。
この積分点を移動する積分方法は、Free Selection Methodと言い 2次元ソリッド、 3次元ソリッド、 3次元ソリッドの固有値計算 のところでも計算例を紹介しています。