■計算精度の検証: その2■
次に数値積分のGauss-Legendre法が有限要素法の中で計算精度が常に保証されているかどうかをチェックしてみます。使うプログラムは4節点要素のFEM4Q.FORです。プログラムの中では積分ルールとしてGauss-Legendre 2点法を使っています。サンプリング点の座標は、ξ=+/-0.577350269です。ここでは、この座標値をξ=+/-0.2から+/-1.0まで変化させ計算結果を厳密解と比較してみました。下図に(x=1,y=1)と(x=2,y=1)の2点での計算精度を示します。縦軸が計算結果(FEM)から厳密解(Exact)を引いた誤差です。横軸がサンプリング点の座標値ξです。

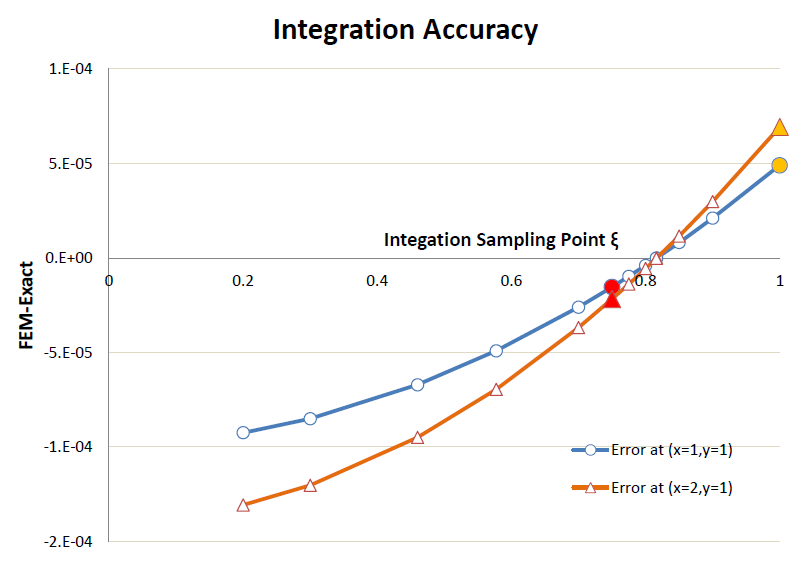
●と▲の点はGauss-Legendre法による誤差です。●と▲の点は台形則による誤差です。この場合、Gauss-Legendre法が常に最高の精度を与えてくれるという保証はありません。確かに要素単位では最高の精度で積分していますが、有限要素法では"剛性マトリクス"を作り上げる過程でAssemby作業があります。この作業により計算精度が落ちてしまいます。これを補正するにはサンプリング点の座標を少し移動するという方法があります。上図を見ると、ξ=+/-0.8165で誤差がほぼゼロになっています。この値を使ったときの計算結果を以下に示します。ND=4*が今回の計算結果です。図では(x=1,y=1)と(x=2,y=1)の2点のみですが、他の節点で精度検証しても同レベルの高い精度でした。