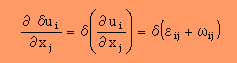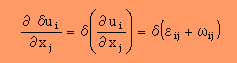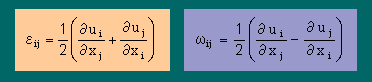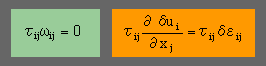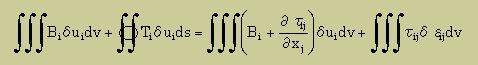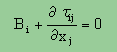Calculus in Finite Element Method
Integration By Parts (2dim & 3dim)-3
上式(前のページ)にあるδuiの微分ですが、次の式に示す様に、strain tensor と rotation tensor の変分の足し算で表すことができます。
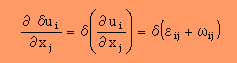 strain tensor と rotation tensor の詳細は、次の様になっています。
strain tensor と rotation tensor の詳細は、次の様になっています。
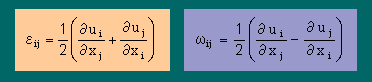 Stress tensor は対称で、rotation tensor は逆対称(skew-symmetry)ですから、下の左の示す様な結果になります。すると、下の右の関係が得られます。
Stress tensor は対称で、rotation tensor は逆対称(skew-symmetry)ですから、下の左の示す様な結果になります。すると、下の右の関係が得られます。
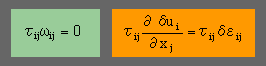 上の結果を仮想仕事の式に代入すると、次の結果が得られます。
上の結果を仮想仕事の式に代入すると、次の結果が得られます。
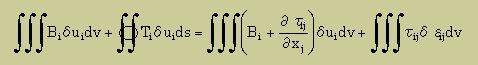 下に示す応力の平衡状態の式 (Navier's equations) を考慮します。
下に示す応力の平衡状態の式 (Navier's equations) を考慮します。
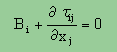 すると、教科書等でよく目にする下の式が出来上がります。"いやー"、頭が痛くなりそうな式ですね。参考までに紹介しておきますが、仮想変位をベースとした仕事量をvirtual work と言い、仮想応力をベースにした式をcomplementary virtual work と言います。
すると、教科書等でよく目にする下の式が出来上がります。"いやー"、頭が痛くなりそうな式ですね。参考までに紹介しておきますが、仮想変位をベースとした仕事量をvirtual work と言い、仮想応力をベースにした式をcomplementary virtual work と言います。

BACK
MENU
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)