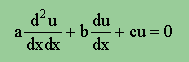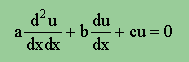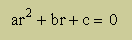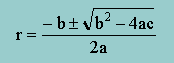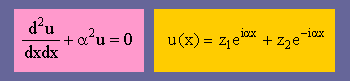■Second Order■
次に2階微分を含む方程式の解き方を紹介します。2階微分項を最高階とする微分方程式を2階微分方程式と言います。 皆さんも知っている通り、下の2階微分方程式の解に sin(x) や cos(x) が有りますね。 と言うことは、sin(x) と cos(x) は、exp(ix) から生まれた関数でしたから、2階微分方程式の解は、複素数で形成されていることになります。 では、早速、下の微分方程式の一般解を導いてみましょう。

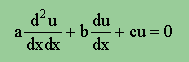まず、解は、u(x)=e^rx だと仮定します。そして、この解を上式に代入すると、下の代数式が残りますね。

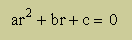この式の解は、皆さんも知っていますね。つまり、下式です。

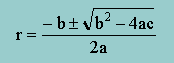例えば、b=0, a=1, c=α² だと、r₁=+iα と r₂=-iα になりますね。 貴方も、そうなるか、確認して下さいね。つまり、下の左の微分方程式の一般解は、その右の様になります。

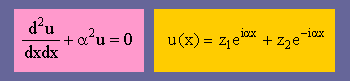ここに、z₁ と z₂ は、境界条件によって決る定数です。 ところで、上の微分方程式を Helmholtz equation と言います。
境界条件と言う新しい言葉が出てきましたね。 基本的に、境界条件には、Dirichlet型とNeumann型が有ります。Dirichlet型は、境界でu(x)の値を指定します。 Neumann型は、du/dx を境界で指定します。例えば、領域の長さが L で、両端がDirichlet型の境界だとします。 そして、x=0 と x=L での境界値をそれぞれ、u(0), u(L) とすると、定数 z₁ と z₂ は、決定できますね。