すると要素内の未知数のu(r,z)とδu(r,z)、更にそれらの微分は、以下のように書けます。
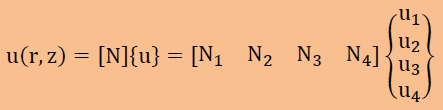
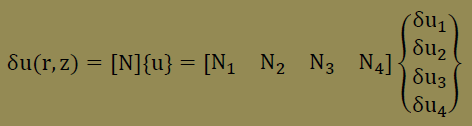
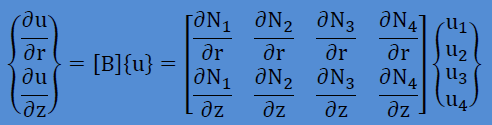
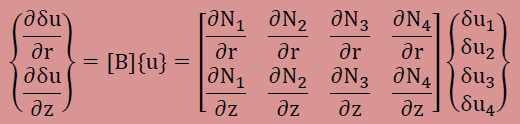
これら全てを積分式に代入すると、以下が得られます。境界積分の項はオミットしてあります。マトリクスの演算[B]T[B]や[N]T[N]についてはマトリクスのページを参考にして下さい。
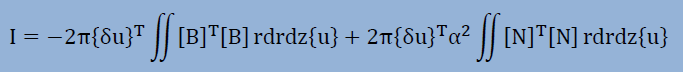
最後にIを{δu}Tで微分し=0と置けば、下に示す有限要素式が得られます。
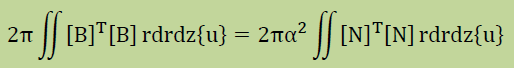
取り扱いを良くするため、上の式を [k]{u}=α2[geom]{u}としておきます。ここに、
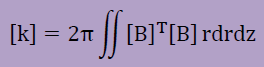
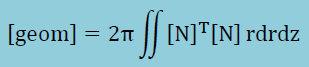
上の式は1つの要素についての結果ですので、同様の積分を計算領域内の全ての要素について行う必要があります。計算領域内には節点数がn個あったとします。そして{u}にはn個の未知数が入っているとします。これをふまえ、上の2つの式を全ての要素に適用しn個の{u}に当てはまるようassemblyするとは以下のような結果が得られます。
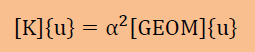
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |