結果的に上の式は固有値問題の連立方程式になっていますので、この連立方程式にShifted Inverse法、Lanczos法、Bisection法を施すと固有値α²を得ることができます。Bisection法の代わりにJacobi法に置き換えても同様に固有値を得ることができます。

■計算例■
容器の注ぎ口に口を当て吹いて音のでる物として試験管やボトルが考えられます。そこで今回は、下の写真に示す4つの器を作りし実験と解析を試みました。器を作る前に所定の周波数が出るように管の長さと体積を決めました。

■計算例1：Test Tube 1■
長さがL=325mmで直径が13mmの試験管の注ぎ口に口を当て吹くと周波数がオクターブ3のドの261Hz近辺のヘルムホルツ共鳴音がするはずです。注ぎ口での圧力変動が試験管の底部で反射し、再び注ぎ口に帰ってきます。注ぎ口で圧力が反転し再び試験管の底部に伝播し、これを繰り返します。この繰り返しで音が出ます。この状況の試験管での基本波、2次波、3次波をグラフで書くと以下になります。ここではこれらの波をDirichlet-Neumann Waveと呼ぶことにします。

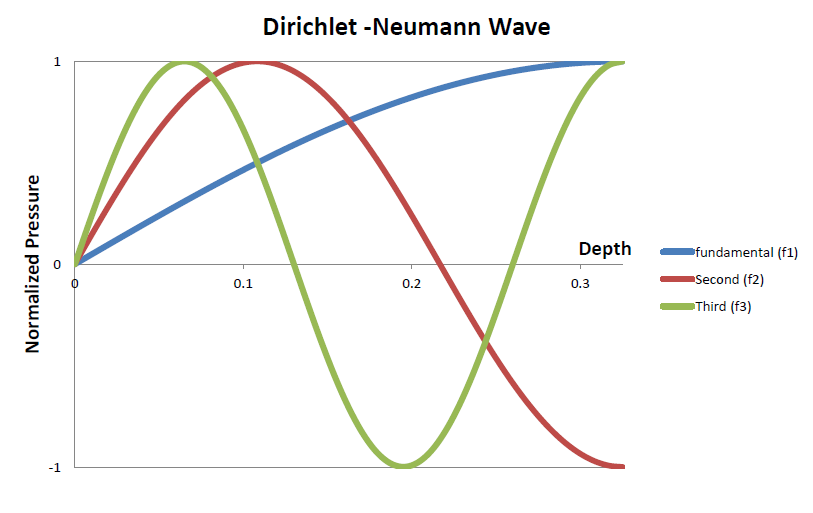
つまり、基本波の場合試験管には波長の1/4が形成(L=λ/4)されていることになります。周波数f、波長λ、音速cとの関係から、f₁=c/(4L)になります。2次波は試験管長(L)に波長の3/4が形成されています。つまり、L=(3/4) λということになります。ですから、f₂=3f1となります。まとめると以下が言えます。