次にHelmholtz equationですが、Wave equationまたは質量保存の式から以下が導き出されました。式中のα2はHelmholtz equationの固有値でα2=ω2/c2です。
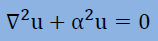
上式をθ方向に変化の無い円筒座標で書くと、以下になります。
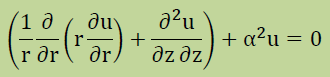
重み付け残差法の手順はこれまでに紹介してきた方法とまったく同じです。違う点は座標系が円筒座標に変わったことです。最初はδuを用いて下に示す積分式を定義します。
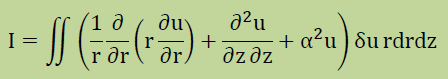
次に2階微分項に部分積分法を施します。この時に発散の定理が必要になります。分かり易くするために項単位で部分積分法を実施します。まず、∂u/∂rの項の部分積分法は、以下になります。
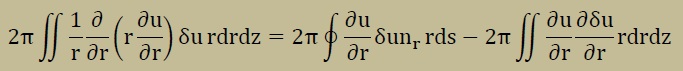
次に∂u/∂zの項に部分積分法を施すと下のようになります。
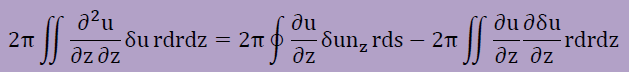
そして全てを足し合わせると、以下の式が得られます。
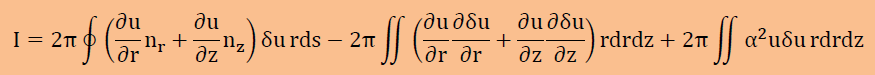
ここで取り上げる音の共鳴問題は、境界で完全反射(∂u/∂n=0)か完全反転(u=0)としますので、上式の境界積分はゼロになります。
次に行う作業は、要素を決め形状関数を書き出します。例えば、4節点bilinear要素の場合、形状関数マトリクス[N]は以下のようになります。詳細についてかParametric要素のページを見て下さい。
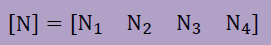
形状関数の微分を表すマトリクス[B]は以下のようになります。
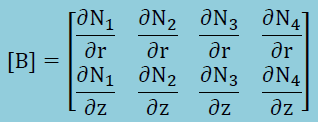
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |