■円筒座標を用いたHelmholtz固有値解析■
Helmholtz equationの固有値を円筒座標で解いてみます。化学実験で使う試験管やワインのボトルの注ぎ口を横から吹くと内部で圧力変動が起き、ある周波数の共鳴音が出ます。前にも言いましたが、この音をHelmholtz共鳴と言います。文献を調べるとこの周波数を求める簡易式が幾つか紹介されています。ここではその共鳴音の固有振動周波数ω[rad/sec]を有限要素法で得られた[K]{u}=α2{u}から計算してみます。固有値α2はLanczos法で部分空間の[T]を導きJacobi法で解いてみます。ω2=c2α2ですから、周波数f[Hz]は、(2πf)2= c2α2で計算できます。また、周期T、音速c、波長λ、周波数fとの関係は、f=1/T, cT=c/f=λ, c=fλ, f=c/λになります。
ここでは、Helmholtz equationが円筒座標でどのように書き表されているか、そして有限要素法はどのように出来ているのかを勉強してみます。
■理論的背景■
円筒座標ですから3次元空間の未知数uを変数のrθzで表すことになります。更に問題を簡略化するために、θ方向の変化は無いものと仮定します。つまり、u=u(r,z)とします。
まず、円筒座標系の発散の定理や支配方程式になれてもらうために、解析学から話をすすめたいと思います。まず、円筒座標系ですが、下図をみて下さい。
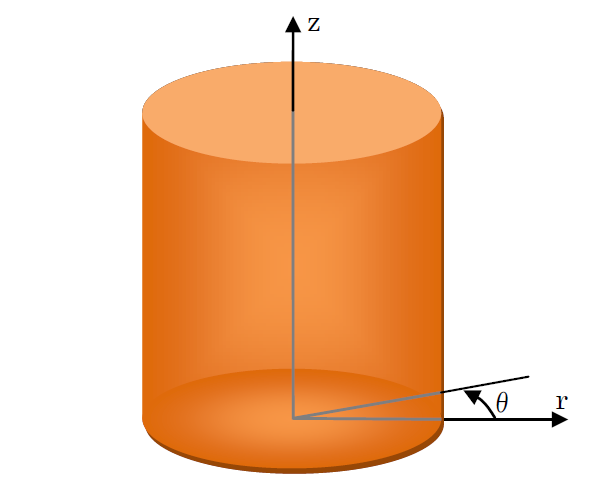
解析学の本を見ますとθ方向の変化がない円筒座標の発散の定理は、以下のようになっています。下の境界積分のdSは上図の側面の場合rdθdzに、上と下面ではrdθdrに該当します。
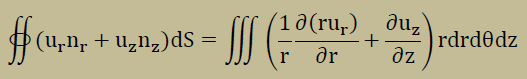
Helmholtz equationでは、未知数がu(r,z)ですからurとuzは以下のように定義できます。
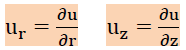
するとHelmholtz equation用の発散の定理は、次のようになります。
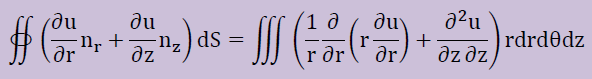
θ方向は積分できますので、最終的に以下が得られます。
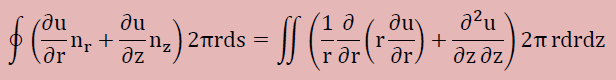
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |